题目内容
设集合A={x|x2-2x≤0，x∈R}，B={y|y=-x2，-1≤x≤2}，则∁R（A∩B）等于（ ）
| A、R | B、{x|x∈R，x≠0} |
| C、{0} | D、φ |
考点：交、并、补集的混合运算
专题：集合
分析：解不等式求出集合A，根据二次函数的图象和性质求出集合B，根据集合交集和补集定义可得答案．
解答：
解：∵集合A={x|x2-2x≤0，x∈R}={x|0≤x≤2}，
B={y|y=-x2，-1≤x≤2}={x|-4≤x≤0}，
∴A∩B={0}，
∴∁R（A∩B）={x|x∈R，x≠0}，
故选：B
B={y|y=-x2，-1≤x≤2}={x|-4≤x≤0}，
∴A∩B={0}，
∴∁R（A∩B）={x|x∈R，x≠0}，
故选：B
点评：本题考查的知识点是集合的交，并，补运算，其中求出集合A，B是解答的关键．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
设集合A={x|-x2+4x-3＞0}，B={x||2x-1|＞3}，则A∩B=（ ）
| A、{x|x＜-1或x＞1} |
| B、{x|x＜-1或x＞2} |
| C、{x|2＜x＜3} |
| D、R |
a=log
3，b=log
2，c=（
）0.3，则（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜c＜a |
| D、b＜a＜c |
设向量
，
满足|
|=|
|=|
+
|=1，则|
-t
|（t∈R）的最小值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||||
B、
| ||||
| C、1 | ||||
D、
|
某报社做了一次关于“什么是新时代的雷锋精神”的调查，在A，B，C，D四个单位回收的问卷数依次成等差数列，且共回收1 000份，因报道需要，再从回收的问卷中按单位分层抽取容量为150的样本，若在B单位抽取30份，则在D单位抽取的问卷份（ ）
| A、60 | B、200 |
| C、400 | D、140 |
正三棱锥的高为1，底面边长为2
，内有一个球与四个面都相切，则棱锥的内切球的半径为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读程序框图，运行相应的程序，则输出i的值为（ ）
| A、3 | B、4 | C、5 | D、6 |
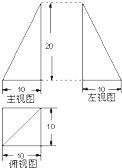某师傅用铁皮制作一封闭的工件，其三视图如图所示（单位长度：cm，图中水平线与竖线垂直），则制作该工件用去的铁皮的面积为（制作过程铁皮的损耗和厚度忽略不计）（ ）A、100（3+
| ||
B、200（3+
| ||
C、300（3+
| ||
| D、300cm2 |