题目内容
设函数f(x)的定义域为D,若任取x1∈D,存在唯一的x2∈D,满足
=C,则称C为函数y=f(x)在D上的均值,给出下列五个函数:①y=x;②y=x2;③y=4sinx;④y=lgx;⑤y=2x.则所有满足在其定义域上的均值为2的函数的序号为( )
| f(x1)+f(x2) |
| 2 |
| A、①③ | B、①④ |
| C、①④⑤ | D、②③④⑤ |
考点:函数的值,函数的图象
专题:函数的性质及应用
分析:根据定义分别验证对于任意的x1∈D,存在唯一的x2∈D,使 f(x1)+f(x2)=4成立的函数即可.
解答:
解:首先分析题目求对于任意的x1∈D,存在唯一的x2∈D,使 f(x1)+f(x2)=4成立的函数.
①y=x,f(x1)+f(x2)=4得 x1+x2=4,解得x2=4-x1,满足唯一性,故成立.
②y=x2,由 f(x1)+f(x2)=4得 x12+x22=4,此时x2=±
,x2有两个值,不满足唯一性,故不满足条件.
③y=4sinx,明显不成立,因为y=4sinx是R上的周期函数,存在无穷个的x2∈D,使
=2成立.故不满足条件
④y=lgx,定义域为x>0,值域为R且单调,显然必存在唯一的x2∈D,使
=2成立.故成立.
⑤y=2x定义域为R,值域为y>0.对于x1=3,f(x1)=8.要使
=2成立,则f(x2)=-4,不成立.
故选:B
①y=x,f(x1)+f(x2)=4得 x1+x2=4,解得x2=4-x1,满足唯一性,故成立.
②y=x2,由 f(x1)+f(x2)=4得 x12+x22=4,此时x2=±
| 4-x12 |
③y=4sinx,明显不成立,因为y=4sinx是R上的周期函数,存在无穷个的x2∈D,使
| f(x1)+f(x2) |
| 2 |
④y=lgx,定义域为x>0,值域为R且单调,显然必存在唯一的x2∈D,使
| f(x1)+f(x2) |
| 2 |
⑤y=2x定义域为R,值域为y>0.对于x1=3,f(x1)=8.要使
| f(x1)+f(x2) |
| 2 |
故选:B
点评:本题主要考查新定义的应用,考查学生的推理和判断能力.综合性较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知角α的顶点是坐标原点,始边是x轴的非负半轴,其终边上有一点P的坐标是(-3,4),则sinα,tanα的值分别是( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
若复数z与2+3i互为共轭复数,则复数z的模|z|=( )
A、
| ||
| B、5 | ||
| C、7 | ||
| D、13 |
复数
为纯虚数,则实数a=( )
| a+i |
| 2-i |
| A、-2 | ||
B、-
| ||
| C、2 | ||
D、
|
命题“?x∈[0,+∞),x2-x+1≥0”的否定是( )
| A、?x∈[0,+∞),x2-x+1<0 |
| B、?x∈(-∞,0),x2-x+1≥0 |
| C、?x0∈[0,+∞),x2-x+1<0 |
| D、?x0∈[0,+∞),x2-x+1≥0 |
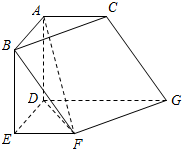 在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.AB=AC=FE=1,DG=2.
在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.AB=AC=FE=1,DG=2.