题目内容
过抛物线y=x2的顶点O任作两条互相垂直的弦OA、OB,若分别以OA、OB为直径作圆,则两圆的另一交点C的轨迹方程为 .
考点:抛物线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:设出A,B坐标;利用向量垂直的充要条件得到A,B纵坐标的乘积是常数;写出以OA,OB为直径的圆;将A,B点的纵坐标看成一个方程的两个根,利用韦达定理表示出A,B的纵坐标乘积;列出等式得到p的轨迹方程.
解答:
解:设A(x1,x12),B(x2,x22),
由于OA⊥OB,即
•
=0,
则x12x22+x1x2=0,即x1•x2=-1①
以OA为直径的圆为x(x-x1)+y(y-x12)=0,
以OB为直径的圆为x(x-x2)+y(y-x22)=0,
设P(x0,y0)为两圆的交点,
所以x1,x2可以看做关于z的方程x0(x0-z)+y0(y0-z2)=0的两个根,
即y0z2+x0z-(x02+y02)=0,
由韦达定理得x1•x2=-
,
结合①得x02+y02=y0,
所以P的轨迹方程是x2+(y-
)2=
(y≠0).
故答案为:x2+(y-
)2=
(y≠0).
由于OA⊥OB,即
| OA |
| OB |
则x12x22+x1x2=0,即x1•x2=-1①
以OA为直径的圆为x(x-x1)+y(y-x12)=0,
以OB为直径的圆为x(x-x2)+y(y-x22)=0,
设P(x0,y0)为两圆的交点,
所以x1,x2可以看做关于z的方程x0(x0-z)+y0(y0-z2)=0的两个根,
即y0z2+x0z-(x02+y02)=0,
由韦达定理得x1•x2=-
| x02+y02 |
| y0 |
结合①得x02+y02=y0,
所以P的轨迹方程是x2+(y-
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:x2+(y-
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查抛物线方程的运用,考查向量垂直的充要条件、以一线段为直径的圆的方程、二次方程的根与系数的关系.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
若θ∈(0,
),则点P(θ-sinθ,θ-tanθ)在( )
| π |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列图形中,不可能是函数图象的是( )
A、 |
B、 |
C、 |
D、 |
倾斜角等于45°,在y轴上的截距等于2的直线方程式( )
| A、y=-x-2 |
| B、y=-x+2 |
| C、y=x-2 |
| D、y=x+2 |
已知幂函数y=f(x)的图象过点(
,
),则f(2)=( )
| 1 |
| 2 |
| ||
| 2 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
若函数f(x)=ax3+bx2+cx+d的图象如图所示,则一定有( )
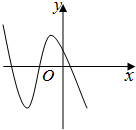

| A、b>0,c>0 |
| B、b<0,c>0 |
| C、b>0,c<0 |
| D、b<0,c<0 |
设函数f(x)的定义域为D,若任取x1∈D,存在唯一的x2∈D,满足
=C,则称C为函数y=f(x)在D上的均值,给出下列五个函数:①y=x;②y=x2;③y=4sinx;④y=lgx;⑤y=2x.则所有满足在其定义域上的均值为2的函数的序号为( )
| f(x1)+f(x2) |
| 2 |
| A、①③ | B、①④ |
| C、①④⑤ | D、②③④⑤ |
设复数z=-
+
i,则
的值为( )
| 1 |
| 2 |
| ||
| 2 |
| |z| |
| z |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|