题目内容
12．若一个边长为a的正三角形，以其中一条高作为轴旋转，则所得旋转体的表面积为（ ）| A． | $\frac{1}{4}$πa2 | B． | $\frac{1}{2}$πa2 | C． | $\frac{3}{4}$πa2 | D． | $\frac{1}{8}$πa2 |
分析 旋转体为底面半径为$\frac{a}{2}$，母线长为a的圆锥．
解答 解：将边长为a的正三角形沿着一条高作为轴旋转旋转得到的几何体为圆锥．
圆锥的底面半径为$\frac{a}{2}$，母线长为a，
∴圆锥的表面积S=$π×（\frac{a}{2}）^{2}+π×\frac{a}{2}×a$=$\frac{3{a}^{2}}{4}$π．
故选：C．
点评 本题考查了圆锥的结构特征的面积计算，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，已知正四棱锥S-ABCD，E、F分别是侧棱SA、SC的中点．求证：
20．若集合A={-2，-1，0，1，2}，B={x|2x＞1}，则A∩B=（ ）
| A． | {-1，2} | B． | {0，1} | C． | {1，2} | D． | {0，1，2} |
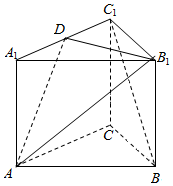已知三棱柱ABC-A1B1C1，△ABC是正三角形，直线AA1⊥平面A1B1C1，D是棱A1C1的中点．