题目内容
3. 如图所示,已知正四棱锥S-ABCD,E、F分别是侧棱SA、SC的中点.求证:
如图所示,已知正四棱锥S-ABCD,E、F分别是侧棱SA、SC的中点.求证:(1)EF∥平面ABCD;
(2)EF⊥平面SBD.
分析 (1)连接BD,运用中位线定理和线面平行的判定定理,即可得证;
(2)由正四棱锥S-ABCD中,AC⊥平面SBD,结合FE∥AC,即可判定EF⊥平面SBD.
解答  证明:(1)连接AC,∵由E、F分别是SA、SC的中点,
证明:(1)连接AC,∵由E、F分别是SA、SC的中点,
∴FE∥AC,
∵EF?平面ABCD,AC?平面ABCD,
∴则有EF∥平面ABCD;
(2)∵正四棱锥S-ABCD中,顶点S在底面的射影为底面中心,
∴AC⊥平面SBD.
∵由(1)可得FE∥AC,
∴EF⊥平面SBD.
点评 本题考查线面平行和垂直的判定和性质,考查空间推理能力,和空间想象能力,属于中档题.

练习册系列答案
相关题目
11.方程$\frac{x^2}{2+m}+\frac{y^2}{m+1}$=1表示双曲线,则m的取值范围是( )
| A. | (-2,-1) | B. | (-2,+∞) | C. | (-∞,-1) | D. | (-∞,-2)∪(-1,+∞) |
15.下列函数中,既是奇函数又在R上单调递减的是( )
| A. | y=$\frac{1}{x}$ | B. | y=e-x | C. | y=-x3 | D. | y=lnx |
12.若一个边长为a的正三角形,以其中一条高作为轴旋转,则所得旋转体的表面积为( )
| A. | $\frac{1}{4}$πa2 | B. | $\frac{1}{2}$πa2 | C. | $\frac{3}{4}$πa2 | D. | $\frac{1}{8}$πa2 |
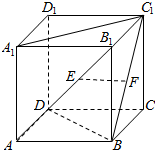 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)