题目内容
一艘海轮从A处出发,以每小时60海里的速度沿东偏南50°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是( )
A、10
| ||
B、10
| ||
C、15
| ||
D、20
|
考点:解三角形的实际应用
专题:计算题,作图题,解三角形
分析:如图,∠DAB=50°,∠DAC=20°,∠CBF=65°;从而在△ABC中化简角,从而利用正弦定理求解.
解答:
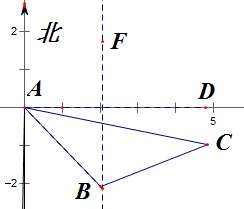 解:如图,∠DAB=50°,∠DAC=20°,∠CBF=65°;
解:如图,∠DAB=50°,∠DAC=20°,∠CBF=65°;
在△ABC中,
∠BAC=∠DAB-∠DAC=50°-20°=30°;
∠ABC=∠ABF+∠CBF=40°+65°=105°;
故∠ACB=180°-105°-30°=45°;
则由正弦定理可得,
=
;
又∵AB=60×
=30海里;
故BC=
×
=15
;
故选C.
 解:如图,∠DAB=50°,∠DAC=20°,∠CBF=65°;
解:如图,∠DAB=50°,∠DAC=20°,∠CBF=65°;在△ABC中,
∠BAC=∠DAB-∠DAC=50°-20°=30°;
∠ABC=∠ABF+∠CBF=40°+65°=105°;
故∠ACB=180°-105°-30°=45°;
则由正弦定理可得,
| AB |
| sin∠ACB |
| BC |
| sin∠BAC |
又∵AB=60×
| 1 |
| 2 |
故BC=
| 30 | ||||
|
| 1 |
| 2 |
| 2 |
故选C.
点评:本题考查了角的化简与转化及正弦定理的应用,同时考查了学生的作图能力,属于中档题.

练习册系列答案
相关题目
已知2a>2b>1,则下列不等关系式中正确的是( )
| A、sina>sinb | ||||
| B、log2a<log2b | ||||
C、(
| ||||
D、(
|
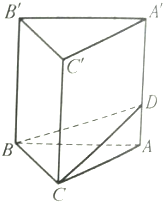 已知正三棱柱的底面边长是4厘米,过BC的一个平面与底面成30°的二面角,交侧棱AA′于D,求AD的长和截面△BCD的面积.
已知正三棱柱的底面边长是4厘米,过BC的一个平面与底面成30°的二面角,交侧棱AA′于D,求AD的长和截面△BCD的面积.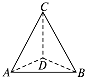
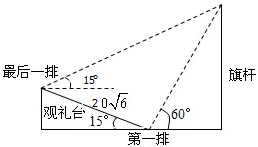 2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一垂直于地面的平面上,在该列的第一排B处和最后一排A处测得旗杆顶端的仰角为15°,且第一排和最后一排的距离为20
2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一垂直于地面的平面上,在该列的第一排B处和最后一排A处测得旗杆顶端的仰角为15°,且第一排和最后一排的距离为20