题目内容
在棱长为1的正方体ABCD-A1B1C1D1中,点E为BB1的中点,则点C1到平面A1ED的距离是 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出点C1到平面A1ED的距离.
解答:
解: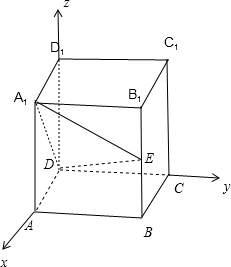 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
D(0,0,0),A1(1,0,1),E(1,1,
),
=(1,0,1),
=(1,1,
),
设平面DAE的法向量
=(x,y,z),
则
,
取x=2,得
=(2,-1,-2),
∵C1(0,1,1),
=(0,1,1),
∴点C1到平面A1ED的距离d=
=
=1.
故答案为:1.
 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
D(0,0,0),A1(1,0,1),E(1,1,
| 1 |
| 2 |
| DA1 |
| DE |
| 1 |
| 2 |
设平面DAE的法向量
| n |
则
|
取x=2,得
| n |
∵C1(0,1,1),
| DC1 |
∴点C1到平面A1ED的距离d=
|
| ||||
|
|
| |0-1-2| |
| 3 |
故答案为:1.
点评:本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知各顶点都在一个球面上的正方体的体积为8,则这个球的表面积是( )
| A、8π | B、12π |
| C、16π | D、20π |
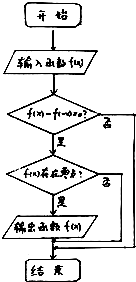 执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )