题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}|{lo{g}_{3}x|,0<x<3}\\{-cos(\frac{π}{3}x),3≤x≤9}\end{array}\right.$,若存在实数x1,x2,x3,x4满足f(xl)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4,则x1•x2•x3•x4的取值范围是(27,$\frac{135}{4}$).分析 画出分段函数的图象,求得(3,1),(9,1),令f(xl)=f(x2)=f(x3)=f(x4)=a,作出直线y=a,通过图象观察,可得a的范围,运用对数的运算性质和余弦函数的对称性,可得x1x2=1,x3+x4=12,再由二次函数在(3,4.5)递增,即可得到所求范围.
解答 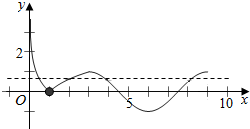 解:解:画出函数f(x)=$\left\{\begin{array}{l}|{lo{g}_{3}x|,0<x<3}\\{-cos(\frac{π}{3}x),3≤x≤9}\end{array}\right.$的图象,
解:解:画出函数f(x)=$\left\{\begin{array}{l}|{lo{g}_{3}x|,0<x<3}\\{-cos(\frac{π}{3}x),3≤x≤9}\end{array}\right.$的图象,
令f(xl)=f(x2)=f(x3)=f(x4)=a,
作出直线y=a,
由x=3时,f(3)=-cosπ=1;x=9时,f(9)=-cos3π=1.
由图象可得,当0<a<1时,直线和曲线y=f(x)有四个交点.
由图象可得0<x1<1<x2<3<x3<4.5,7.5<x4<9,
则|log3x1|=|log3x2|,即为-log3x1=log3x2,可得x1x2=1,
由y=-cos($\frac{π}{3}$x)的图象关于直线x=6对称,可得x3+x4=12,
则x1•x2•x3•x4=x3(12-x3)=-(x3-6)2+36在(3,4.5)递增,
即有x1•x2•x3•x4∈(27,$\frac{135}{4}$).
故答案为:(27,$\frac{135}{4}$).
点评 本题考查分段函数的图象及运用,考查数形结合的思想方法,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
5.已知复数z=i,则$\frac{1}{z+1}$的虚部为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}i$ |
12.已知数列{an}满足a1=0,an+1=an+2n,则a2015等于( )
| A. | 2014×2013 | B. | 2015×2014 | C. | 2013×2012 | D. | 2015×2016 |
9.函数f(x)=$\sqrt{tanx-1}$的定义域是( )
| A. | $[{\frac{π}{4}+kπ,+∞}),k∈Z$ | B. | $[{\frac{π}{4}+kπ,\frac{π}{2}+kπ}),k∈Z$ | C. | $[{\frac{π}{4}+kπ,\frac{π}{2}+kπ}]$,k∈Z | D. | $[{\frac{π}{4},\frac{π}{2}})$ |