执行如图所示的程序框图.输出S的值为$\frac{1}{2}$时.k是( )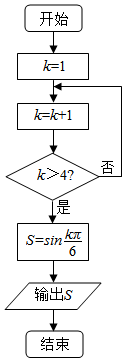A．5B．3C．4D．2 题目和参考答案——青夏教育精英家教网—

题目内容

8．执行如图所示的程序框图，输出S的值为$\frac{1}{2}$时，k是（　　）

A．

B．

C．

D．

分析模拟执行程序，依次写出每次循环k的值，当k=5时，大于4，计算输出S的值为$\frac{1}{2}$，从而得解．

解答解：模拟执行程序，可得每次循环的结果依次为：
k=2，k=3，k=4，k=5，大于4，
可得S=sin$\frac{5π}{6}$=$\frac{1}{2}$，
输出S的值为$\frac{1}{2}$．
故选：A．

点评本题主要考查了循环结果的程序框图，模拟执行程序正确得到k的值是解题的关键，属于基础题．

练习册系列答案

1．计算：i²⁰¹⁰+（$\sqrt{2}$+$\sqrt{2}i$）²-（$\frac{\sqrt{2}}{1-i}$）⁴．

18．假知生化危机爆发，有10个人被困在超市内，超市内除了固定的食物，每天还有军方空投定量的食物，超市内的人坚持22天之后断粮，如过被困者数量是16人，那么他们在同样的悄况下却只能坚持10天．
请问：如果被困者是25人，他们可以坚持多少天？

3．二项式（$\frac{x}{\sqrt{2}}$-y）⁸的展开式中，x⁴y⁴与x²y⁶项的系数之和是$\frac{63}{2}$（用数字作答）

13．下列命题：
①已知m，n表示两条不同的直线，α，β表示两个不同的平面，并且m⊥α，n?β，则“α⊥β”是“m∥n”的必要不充分条件；
②不存在x∈（0，1），使不等式成立log₂x＜log₃x；
③“若am²＜bm²，则a＜b”的逆命题为真命题；
④?θ∈R，函数f（x）=sin（2x+θ）都不是偶函数．
正确的命题序号是①．

20．设命题p：?x₀∈（0，+∞），${3^{x_0}}＜x_0^3$，则命题p的否定为（　　）

17．某集成电路由2个不同的电子元件组成．每个电子元件出现故障的概率分别为$\frac{1}{6}，\frac{1}{10}$．两个电子元件能否正常工作相互独立，只有两个电子元件都正常工作该集成电路才能正常工作．
（1）求该集成电路不能正常工作的概率；
（2）如果该集成电路能正常工作，则出售该集成电路可获利40元；如果该集成电路不能正常工作，则每件亏损80元（即获利-80元）．已知一包装箱中有4块集成电路，记该箱集成电路获利x元，求x的分布列，并求出均值E（x）．

18．已知f（x）=2sin（2x+$\frac{π}{6}$），若将它的图象向右平移$\frac{π}{6}$个单位，得到函数g（x）的图象，则函数g（x）的图象的一个对称中心为（　　）

试题分类