题目内容
已知f(x)=
，则函数g（x）=f（x）-ex的零点个数为（ ）
|
| A、1 | B、2 | C、3 | D、4 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：设y=ex，y=f（x），分别作出两个函数的图象，利用图象的交点个数，确定函数零点的个数．
解答：
解：函数g（x）=f（x）-ex的零点，
即为函数y=ex，y=f（x）交点的横坐标，
在同一坐标系中画出y=ex，y=f（x）=
的图象如下图所示：
，
由图象可知两个函数有2个交点，
即函数g（x）=f（x）-ex的零点个数为2个．
故选：B．
即为函数y=ex，y=f（x）交点的横坐标，
在同一坐标系中画出y=ex，y=f（x）=
|
，由图象可知两个函数有2个交点，
即函数g（x）=f（x）-ex的零点个数为2个．
故选：B．
点评：本题主要考查函数与方程之间的关系，利用数形结合是解决函数交点问题中最基本的方法，要求熟练掌握．
练习册系列答案
相关题目
若三点P（1，1），A（2，-4），B（x，-14）共线，则（ ）
| A、x=-1 | B、x=3 |
| C、x=4 | D、x=51 |
正方形ABCD的边长为3，点E在边AB上，点F在边BC上，AE=BF=1，动点P从点E出发沿直线向F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当点P第一次碰到点E时，P与正方形的边碰撞的次数为（ ）
| A、8 | B、6 | C、4 | D、3 |
用反证法证明：“若a，b，c都是正数，则三个数a+
，b+
，c+
中至少有一个不小于2”时，“假设”应为（ ）
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
A、假设a+
| ||||||
B、假设a+
| ||||||
C、假设a+
| ||||||
D、假设a+
|
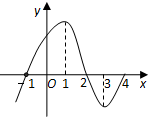如图所示为y=f′（x）的图象，则下列判断正确的是（ ）①f（x）在（-∞，1）上是增函数；
②x=-1是f（x）的极小值点；
③f（x）在（2，4）上是减函数，在（-1，2）上是增函数；
④x=2是f（x）的极小值点．
| A、①②③ | B、①③④ |
| C、③④ | D、②③ |
设f（x）=x2-2x-4lnx，则f（x）的增区间为（ ）
| A、（0，+∞） |
| B、（2，+∞） |
| C、（-∞，-1） |
| D、（∞，-1）和（2，+∞） |
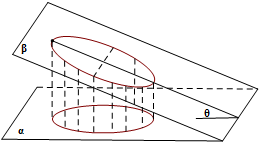如图，一个底面半径为R的圆柱被与其底面所成角为θ（00＜θ＜900）的平面所截，截面是一个椭圆．当θ为30°时，这个椭圆的离心率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|