Question

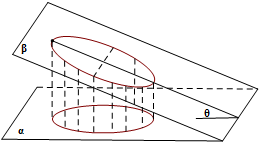如图，一个底面半径为R的圆柱被与其底面所成角为θ（0⁰＜θ＜90⁰）的平面所截，截面是一个椭圆．当θ为30°时，这个椭圆的离心率为（　　）

• A、

  1

  2

• B、

  3

  2

• C、

  3

  3

• D、

  2

  3

Answer 1

考点：平面与圆柱面的截线

专题：计算题,圆锥曲线的定义、性质与方程

分析：利用已知条件，求出题意的长半轴，短半轴，然后求出半焦距，即可求出题意的离心率．

解答： 解：因为底面半径为R的圆柱被与底面成30°的平面所截，其截口是一个椭圆，
则这个椭圆的短半轴为：R，长半轴为：

R

cos30°

=

2R

3

，
∵a²=b²+c²，∴c=

R

3

，
∴椭圆的离心率为：e=

c

a

=

1

2

．
故选：A．

点评：本题考查椭圆离心率的求法，注意椭圆的几何量与双曲线的几何量（a，b，c）关系的正确应用，考查计算能力．