题目内容
已知奇函数f（x）在（0，+∞）上为减函数，且f（3）=0，求
＜0．
| f(x) |
| x |
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据函数的奇偶性和单调性之间的关系，将不等式进行转化即可得到解不等式的解集．
解答：
解：∵奇函数f（x）在（0，+∞）上为减函数，
∴f（x）在（-∞，0）上为减函数，
∵f（3）=0，∴f（-3）=-f（3）=0，
∴当x＞3或-3＜x＜0时，f（x）＜0，
当x＜-3或0＜x＜3时，f（x）＞0，
∴不等式
＜0．
等价为当x＞0时f（x）＜0，此时x＞3，
当x＜0时，f（x）＞0，此时x＜-3．
故不等式的解集为{x|x＞3或x＜-3}．
∴f（x）在（-∞，0）上为减函数，
∵f（3）=0，∴f（-3）=-f（3）=0，
∴当x＞3或-3＜x＜0时，f（x）＜0，
当x＜-3或0＜x＜3时，f（x）＞0，
∴不等式
| f(x) |
| x |
等价为当x＞0时f（x）＜0，此时x＞3，
当x＜0时，f（x）＞0，此时x＜-3．
故不等式的解集为{x|x＞3或x＜-3}．
点评：本题主要考查函数奇偶性和单调性的性质，根据函数性质的综合应用，将不等式转化是解决本题的关键．
练习册系列答案
53随堂测系列答案
相关题目
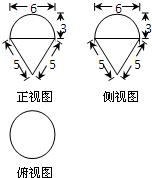一个几何体的三视图如图所示，它的体积为（ ）| A、24π | B、30π |
| C、48π | D、72π |