题目内容
计算图形:y=x2+1与y=6所围成的区域面积.
考点:定积分在求面积中的应用
专题:导数的综合应用
分析:作出曲线对应的图形,联立方程组求解交点的横坐标,然后利用积分的几何意义即可求区域面积.
解答:
 解:当y=6时,由y=x2+1=6,
解:当y=6时,由y=x2+1=6,
即x2=5,即x=±
,
则由积分的几何意义可知所求区域的面积为S=
(6-x2-1)dx=
(5-x2)dx=(5x-
x3)
=(5
-
(
)3)-(-5
+
(
)3)=
.
 解:当y=6时,由y=x2+1=6,
解:当y=6时,由y=x2+1=6,即x2=5,即x=±
| 5 |
则由积分的几何意义可知所求区域的面积为S=
| ∫ |
-
|
| ∫ |
-
|
| 1 |
| 3 |
| | |
-
|
=(5
| 5 |
| 1 |
| 3 |
| 5 |
| 5 |
| 1 |
| 3 |
| 5 |
20
| ||
| 3 |
点评:本题主要考查利用函数的积分求区域面积,要求熟练掌握常见函数的积分公式.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
函数f(x)=(sinx+cosx)2的最小正周期为( )
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
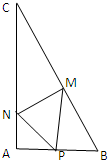 在Rt△ABC中,AB=2,AC=4,∠A为直角,P为AB中点,M、N分别是BC,AC上任一点,则△MNP周长的最小值是
在Rt△ABC中,AB=2,AC=4,∠A为直角,P为AB中点,M、N分别是BC,AC上任一点,则△MNP周长的最小值是