题目内容
函数y=
的最大值为 ．
| x(4-x) |
考点：函数的值域
专题：函数的性质及应用
分析：首先把二次函数转化成标准型，进一步利用定义域求出函数的最值．
解答：
解：函数y=
=
=
函数的定义域{x|0＜x＜4}
所以：当x=2时，函数取最小值
所以：ymin=2
故答案为：2
| x(4-x) |
| -x2+4x |
| -(x-2)2+4 |
函数的定义域{x|0＜x＜4}
所以：当x=2时，函数取最小值
所以：ymin=2
故答案为：2
点评：本题考查的知识要点：二次函数的性质的应用，属于基础题型．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知函数f（x）的定义域为R，则“f（x）在[-2，2]上单调递增”是“f（-2）＜f（2）”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若复数z=
，则|z|=（ ）
| 2 | ||
1+
|
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
函数f（x）=log2（x+1）的定义域为（ ）
| A、（0，+∞） |
| B、[-1，+∞） |
| C、（-1，+∞） |
| D、（1，+∞） |
命题“?x∈R+，lnx＞0”的否定是（ ）
| A、?x∈R+，lnx＞0 |
| B、?x∈R+，lnx≤0 |
| C、?x∈R+，lnx＞0 |
| D、?x∈R+，lnx≥0 |
x，y满足约束条件
，若z=y-2ax取得最大值的最优解不唯一，则实数a的值为（ ）
|
A、1或-
| ||
B、
| ||
| C、2或1 | ||
| D、2或-1 |
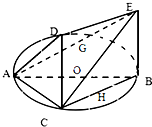如图，一简单几何体ABCDE的一个面ABC内接于圆O，G、H分别是AE、BC的中点，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．