题目内容
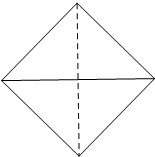已知四面体S-ABC的所有棱长都相等，它的俯视图如图所示，是一个边长为| 2 |
| A、6π | B、4π | C、8π | D、3π |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：由三视图可知：该四面体是正方体的一个内接正四面体．此四面体的外接球的半径为正方体的对角线长=
．利用球的表面积计算公式即可得出．
| 6 |
解答：
解：由三视图可知：该四面体是正方体的一个内接正四面体．
∴此四面体的外接球的直径为正方体的对角线长=
．
∴此四面体的外接球的表面积为表面积=4π×(
)2=6π．
故选：A．
解：由三视图可知：该四面体是正方体的一个内接正四面体．∴此四面体的外接球的直径为正方体的对角线长=
| 6 |
∴此四面体的外接球的表面积为表面积=4π×(
| ||
| 2 |
故选：A．
点评：本题考查了三棱锥的三视图、正方体与外接球的性质、球的表面积的计算公式，考查了推理能力与空间想象能力、计算能力，属于中档题．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知向量
=(cos2α，
)，
=(
，sin2α)，且-
≤α≤
，则“α=
”是“
⊥
”的（ ）
| a |
| ||
| 2 |
| b |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 12 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知一个程序框图如图所示，若输入n=6，则该程序运行的结果是（ ）
| A、2 | B、3 | C、4 | D、15 |
已知抛物线的一条过焦点F的弦PQ，点R在直线PQ上，且满足
=
（
+
），R在抛物线准线上的射影为S，设α，β是△PQS中的两个锐角，则下列四个式子中不一定正确的是（ ）
| OR |
| 1 |
| 2 |
| OP |
| OQ |
| A、tanαtanβ=1 | ||
B、sinα+sinβ≤
| ||
| C、cosα+cosβ＞1 | ||
D、|tan（α-β）|＞tan
|