题目内容
已知抛物线的一条过焦点F的弦PQ,点R在直线PQ上,且满足
=
(
+
),R在抛物线准线上的射影为S,设α,β是△PQS中的两个锐角,则下列四个式子中不一定正确的是( )
| OR |
| 1 |
| 2 |
| OP |
| OQ |
| A、tanαtanβ=1 | ||
B、sinα+sinβ≤
| ||
| C、cosα+cosβ>1 | ||
D、|tan(α-β)|>tan
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:让PQ⊥x轴,并且取α,β=45°,容易验证D不成立.
解答:
解:根据已知条件,R为PQ中点,可取α,β都为45°的情况进行验证,图形如下:
 显然D不成立.
显然D不成立.
故选D.
 显然D不成立.
显然D不成立.故选D.
点评:考查抛物线的焦点,准线方程,以及利用特殊情况验证选项是否成立的方法.

练习册系列答案
相关题目
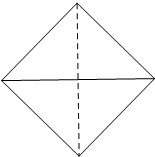 已知四面体S-ABC的所有棱长都相等,它的俯视图如图所示,是一个边长为
已知四面体S-ABC的所有棱长都相等,它的俯视图如图所示,是一个边长为| 2 |
| A、6π | B、4π | C、8π | D、3π |
函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于( )
| A、2 | B、3 | C、4 | D、5 |
函数f(x)=ex+e-x的图象大致为( )
A、 |
B、 |
C、 |
D、 |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<