题目内容
已知圆C的极坐标方程为ρ=2cosθ，直线l的极坐标方程为θ=
，则圆心到直线l的距离等于 ．
| π |
| 3 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把极坐标方程分别化为直角坐标方程，再利用点到直线的距离公式即可得出．
解答：
解：由圆C的极坐标方程为ρ=2cosθ，可得ρ2=2ρcosθ，化为x2+y2=2x，∴（x-1）2+y2=1，可得圆心C（1，0）．
直线l的极坐标方程为θ=
，可得直角坐标方程：y=
x．
∴圆心到直线l的距离d=
=
．
故答案为：
．
直线l的极坐标方程为θ=
| π |
| 3 |
| 3 |
∴圆心到直线l的距离d=
| ||||
|
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查了把极坐标方程分别化为直角坐标方程、点到直线的距离公式，考查了计算能力，属于基础题．
练习册系列答案
相关题目
如图，已知AF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=2，AB=4．
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜已知
=（2，1，-3），
=（-1，2，3），
（7，6，λ），若
，
，
三向量共面，则λ=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| A、9 | B、-9 | C、-3 | D、3 |
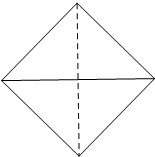已知四面体S-ABC的所有棱长都相等，它的俯视图如图所示，是一个边长为| 2 |
| A、6π | B、4π | C、8π | D、3π |