题目内容
7.已知二面角α-l-β=60°,平面α内一点M到β的距离是$\sqrt{3}$,求M在β上的投影M′到棱l的距离.分析 过M作AM′⊥β垂足为M′,则MM′=$\sqrt{3}$,作MH⊥l,垂足为H,连接HM′,则l⊥M′H,∠MHM′为锐二面角α-l-β的平面角,在直角△MHM′中求解即可.
解答 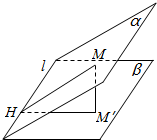 解:过M作AM′⊥β垂足为M′,则MM′=$\sqrt{3}$,作MH⊥l,垂足为H,连接HM′,
解:过M作AM′⊥β垂足为M′,则MM′=$\sqrt{3}$,作MH⊥l,垂足为H,连接HM′,
则l⊥M′H,∠MHM′为锐二面角α-l-β的平面角,
在直角△MHM′中,sin∠MHM′=$\frac{\sqrt{3}}{MH}$=$\frac{\sqrt{3}}{2}$,
∴M′H=2.
点评 本题考查二面角的大小度量,考查转化、空间想象、计算能力.本题找出,∠MHM′为锐二面角α-l-β的平面是关键.

练习册系列答案
相关题目
18.一个椭圆的半焦距为2,离心率e=$\frac{2}{3}$,则它的短轴长是( )
| A. | 3 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 6 |
15.如图,正方体中,两条异面直线BC1与B1D1所成的角是( )
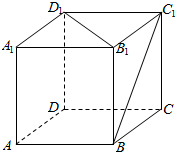

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
2.已知函数f(x)=$\left\{\begin{array}{l}{|lgx|,0<x≤3}\\{f(6-x),3<x<6}\end{array}\right.$,设方程f(x)=2-x+b(b∈R)的四个实根从小到大依次为x1,x2,x3,x4,对于满足条件的任意一组实根,下列判断中一定正确的为( )
| A. | x1+x2=2 | B. | 9<x3•x4<25 | C. | 0<(6-x3)•(6-x4)<1 | D. | 1<x1•x2<9 |
12.与函数y=|x|相等的函数是( )
| A. | y=($\sqrt{x}$)2 | B. | y=($\root{3}{x}$)3 | C. | y=$\sqrt{{x}^{2}}$ | D. | y=$\root{3}{{x}^{3}}$ |
17.某中学高一、高二各有一个文科和一个理科两个实验班,现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每个班级去一所高校,每所高校至少有一个班级去,则恰好有一个文科班和一个理科班分配到上海交通大学的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |