题目内容
12.与函数y=|x|相等的函数是( )| A. | y=($\sqrt{x}$)2 | B. | y=($\root{3}{x}$)3 | C. | y=$\sqrt{{x}^{2}}$ | D. | y=$\root{3}{{x}^{3}}$ |
分析 对于A,B,D经过化简都可得到y=x,显然对应法则和y=|x|的不同,即与y=|x|不相等,而C化简后会得到y=|x|,从而得出该函数和y=|x|相等.
解答 解:y=$(\sqrt{x})^{2}=x$,$y=(\root{3}{x})^{3}=x$,$y=\root{3}{{x}^{3}}$=x,这几个函数的对应法则和y=|x|的不同,不是同一函数;
$y=\sqrt{{x}^{2}}=|x|$,定义域和对应法则都相同,是同一函数.
故选C.
点评 考查函数的三要素:定义域、值域,和对应法则,三要素中有一要素不同,便不相等,而只要定义域和对应法则相同时,两函数便相等.

练习册系列答案
相关题目
3.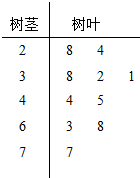 我国政府对PM2.5采用如下标准:某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
我国政府对PM2.5采用如下标准:某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
(1)求这10天数据的中位数;
(2)从这10天数据中任取4天的数据,记ξ为空气质量达到一级的天数,求ξ的分布列和期望;
(3)以这10天的数据来估计这一年365天的空气质量情况,并假定每天之间的空气质量相互不影响.记η为这一年中空气质量达到一级的天数,求η的平均值.
 我国政府对PM2.5采用如下标准:某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
我国政府对PM2.5采用如下标准:某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).| PM2.5日均值m(微克/立方米) | 空气质量等级 |
| m<35 | 一级 |
| 35≤m≤75 | 二级 |
| m>75 | 超标 |
(2)从这10天数据中任取4天的数据,记ξ为空气质量达到一级的天数,求ξ的分布列和期望;
(3)以这10天的数据来估计这一年365天的空气质量情况,并假定每天之间的空气质量相互不影响.记η为这一年中空气质量达到一级的天数,求η的平均值.
1.设a、b为两条不同的直线,α、β为两个不同的平面,则下列命题中为真命题的是( )
| A. | 若a⊥α,α⊥β,则a∥β | B. | 若a∥α,b∥α,则a∥b | C. | 若a∥α,α⊥β,则a⊥β | D. | 若a⊥α,a∥β,则α⊥β |
2.一个三棱锥的三视图如图所示,则它的体积为( )
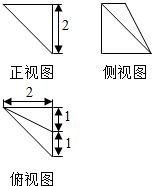

| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |