题目内容
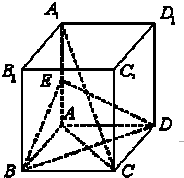 如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点.
如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点.(Ⅰ)求证:A1C∥平面BDE;
(Ⅱ)求证:平面A1AC⊥平面BDE;
(Ⅲ)求直线BE与平面A1AC所成角的正弦值.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)根据线面平行的判定定理即可证明A1C∥平面BDE;
(Ⅱ)根据面面垂直的判定定理即可证明平面A1AC⊥平面BDE;
(Ⅲ)求出直线BE与平面A1AC所成角,然后根据三角形的边角关系即可求出结论.
(Ⅱ)根据面面垂直的判定定理即可证明平面A1AC⊥平面BDE;
(Ⅲ)求出直线BE与平面A1AC所成角,然后根据三角形的边角关系即可求出结论.
解答:
解:(Ⅰ)设AC∩BD=O,
∵E、O分别是AA1、AC的中点,
∴A1C∥EO
又A1C?平面BDE,EO?平面BDE,
∴A1C∥平面BDE
(Ⅱ)∵AA1⊥平面ABCD,BD?平面ABCD,AA1⊥BD,
又BD⊥AC,AC∩AA1=A,
∴BD⊥平面A1AC,
BD?平面BDE,
∴平面BDE⊥平面A1AC
(Ⅲ)由(Ⅱ)可知直线BE与平面A1AC所成角是∠BEO
设正方体棱长为a,在Rt△BOE中,EO=
a,BE=
a,
∴sin∠BEO=
即直线BE与平面A1AC所成角的正弦值为
.
∵E、O分别是AA1、AC的中点,
∴A1C∥EO

又A1C?平面BDE,EO?平面BDE,
∴A1C∥平面BDE
(Ⅱ)∵AA1⊥平面ABCD,BD?平面ABCD,AA1⊥BD,
又BD⊥AC,AC∩AA1=A,
∴BD⊥平面A1AC,
BD?平面BDE,
∴平面BDE⊥平面A1AC
(Ⅲ)由(Ⅱ)可知直线BE与平面A1AC所成角是∠BEO
设正方体棱长为a,在Rt△BOE中,EO=
| ||
| 2 |
| ||
| 2 |
∴sin∠BEO=
| ||
| 5 |
| ||
| 5 |
点评:本题主要考查线面平行和面面垂直的判断以及直线和平面所成角的求解,要求熟练掌握相应的判定定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
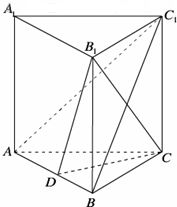 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=AA1,
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=AA1,