题目内容
现有8名青年,其中有5名能胜任英语翻译工作;有4名青年能胜任德语翻译工作(其中有1名青年两项工作都能胜任),现在要从中挑选5名青年承担一项任务,其中3名从事英语翻译工作,2名从事德语翻译工作,则有多少种不同的选法?
考点:排列、组合及简单计数问题
专题:排列组合
分析:根据题意,设能胜任两种工作的那个人为A,进而分3类讨论:不选派A;A被选为英语翻译工作;A被选为德语翻译工作;分别求出其情况数目,由分类计数原理,计算可得答案.
解答:
解:设能胜任两种工作的那个人为A,
记为A不选派A的方法数C43C32=12;
A被选为英语翻译工作的方法数C42C32=18;
A被选为德语翻译工作的方法数 C43C31=12,
故不同的选法种数为42,
记为A不选派A的方法数C43C32=12;
A被选为英语翻译工作的方法数C42C32=18;
A被选为德语翻译工作的方法数 C43C31=12,
故不同的选法种数为42,
点评:本题考查排列、组合的运用,关键在于分析两种工作都能胜任的参加者,对其参与的情况分类讨论.

练习册系列答案
相关题目
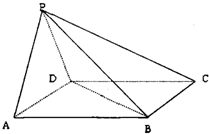 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=