题目内容
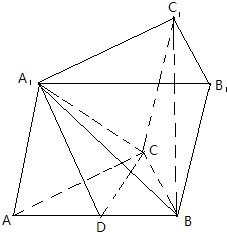 如图,在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1,A1B=
如图,在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1,A1B=| 2 |
(1)求证:平面A1BC⊥平面ACC1A1;
(2)若D为AB中点,求证:BC1∥平面A1CD;
(3)若D为AB得三等分点,且
| AD |
| DB |
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)利用等边三角形的判定、勾股定理的逆定理、及线面、面面垂直的判定定理和性质定理即可证明;
(2)利用平行四边形的性质、三角形的中位线定理、线面平行的判定定理即可证明;
(3)V左=
•2S•h=
Sh,V柱=3Sh,V右=3Sh-
Sh=
Sh,即可求出平面A1CD将三棱柱分成左,右两部分体积的比.
(2)利用平行四边形的性质、三角形的中位线定理、线面平行的判定定理即可证明;
(3)V左=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
解答:
 (1)证明:在△A1AC中,∠A1AC=60°,AA1=AC=1,
(1)证明:在△A1AC中,∠A1AC=60°,AA1=AC=1,
∴A1C=1,
在△A1BC中,BC=1,A1C=1,A1B=
,
∴∠A1BC=90°,∴BC⊥A1C,
又AA1⊥BC,AA1∩A1C=A1,
∴BC⊥平面ACC1A1,
∵BC?平面A1BC,
∴平面A1BC⊥平面ACC1A1.
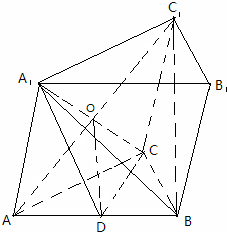
(2)证明:连接A1C交AC1于O,连接DO
则由D为AB中点,O为AC1中点得,OD∥BC1,
∵OD?平面A1DC,BC1?平面A1DC,
∴BC1∥平面A1DC;
(3)解:记S△CBD=S,则S△CAD=2S,S△CAB=2S,棱柱的高为h,则
V左=
•2S•h=
Sh,V柱=3Sh,V右=3Sh-
Sh=
Sh,
∴平面A1CD将三棱柱分成左,右两部分体积的比为2:7.
 (1)证明:在△A1AC中,∠A1AC=60°,AA1=AC=1,
(1)证明:在△A1AC中,∠A1AC=60°,AA1=AC=1,∴A1C=1,
在△A1BC中,BC=1,A1C=1,A1B=
| 2 |
∴∠A1BC=90°,∴BC⊥A1C,
又AA1⊥BC,AA1∩A1C=A1,
∴BC⊥平面ACC1A1,
∵BC?平面A1BC,
∴平面A1BC⊥平面ACC1A1.
(2)证明:连接A1C交AC1于O,连接DO
则由D为AB中点,O为AC1中点得,OD∥BC1,
∵OD?平面A1DC,BC1?平面A1DC,
∴BC1∥平面A1DC;
(3)解:记S△CBD=S,则S△CAD=2S,S△CAB=2S,棱柱的高为h,则
V左=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
∴平面A1CD将三棱柱分成左,右两部分体积的比为2:7.
点评:熟练掌握等边三角形的判定、勾股定理的逆定理、及线面、面面垂直与平行的判定定理和性质定理、平行四边形的性质、三角形的中位线定理是证明问题的关键.

练习册系列答案
相关题目
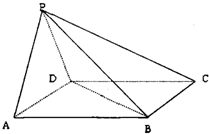 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=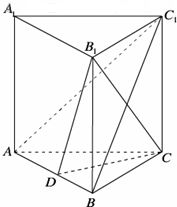 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=AA1,
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC=AA1,