题目内容
17.已知圆锥的底面直径与高都是2,则该圆锥的侧面积为$\sqrt{5}π$.分析 首先根据底面半径和高利用勾股定理求得母线长,然后直接利用圆锥的侧面积公式代入求出即可.
解答 解:∵圆锥的底面直径与高都是2,
∴母线长为:$\sqrt{1+4}$=$\sqrt{5}$,
∴圆锥的侧面积为:πrl=$\sqrt{5}π$.
故答案为:$\sqrt{5}π$.
点评 本题考查了圆锥的侧面积的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键.

练习册系列答案
相关题目
8.昌平区在滨河公园举办中学生冬季越野赛.按年龄段将参赛学生分为A,B,C三个组,各组人数如下表所示.组委会用分层抽样的方法从三个组中选出6名代表.
( I) 求A,B,C三个组各选出代表的个数;
( II) 若从选出的6名代表中随机抽出2人在越野赛闭幕式上发言,求这两人来自同一组的概率P1;
( III)若从所有参赛的300名学生中随机抽取2人在越野赛闭幕式上发言,设这两人来自同一组的概率为P2,试判断P1与P2的大小关系(不要求证明).
| 组别 | A | B | C |
| 人数 | 100 | 150 | 50 |
( II) 若从选出的6名代表中随机抽出2人在越野赛闭幕式上发言,求这两人来自同一组的概率P1;
( III)若从所有参赛的300名学生中随机抽取2人在越野赛闭幕式上发言,设这两人来自同一组的概率为P2,试判断P1与P2的大小关系(不要求证明).
7.若过椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的上顶点与右焦点的直线l,则该椭圆的左焦点到直线l的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
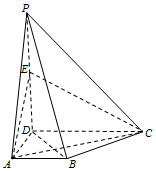 如图,在四棱锥P-ABCD 中,PD⊥底面ABCD,AB∥DC,CD=2AB,AD⊥CD,E为棱PD的中点.
如图,在四棱锥P-ABCD 中,PD⊥底面ABCD,AB∥DC,CD=2AB,AD⊥CD,E为棱PD的中点.