题目内容
9.如图,AB为半圆O的直径,D为弧BC的中点,E为BC的中点,求证:AB•BC=2AD•BD.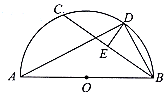
分析 证明△ABD∽△BDE,即可证明结论.
解答 证明:因为D为弧BC的中点,所以∠DBC=∠DAB,DC=DB,
因为AB为半圆O的直径,所以∠ADB=90°,
又E为BC的中点,所以EC=EB,所以DE⊥BC,
所以△ABD∽△BDE,
所以$\frac{AB}{AD}=\frac{BD}{BE}=\frac{2BD}{BC}$,所以AB•BC=2AD•BD.…(10分)
点评 本题考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.下列四个函数中,在其定义域上既是奇函数又是单调递增函数的是( )
| A. | y=ex | B. | y=sinx | C. | $y=\sqrt{x}$ | D. | y=x3 |
14.某四棱锥的三视图如图所示,该四棱锥的四个侧面的面积中最大的是( )
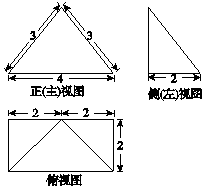

| A. | 3 | B. | $2\sqrt{5}$ | C. | 6 | D. | $3\sqrt{5}$ |
19.曲线f(x)=$\frac{1}{3}$x3-2在点(-1,f(-1))处切线的斜率为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
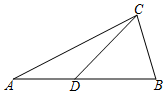 如图所示,点D 在线段AB 上,∠CAD=30°,∠CDB=50°.给出下列三组条件(给出线段的长度):
如图所示,点D 在线段AB 上,∠CAD=30°,∠CDB=50°.给出下列三组条件(给出线段的长度):