题目内容
设函数f(x)=sinxcosx,x∈R,则函数f(x)的最小值是( )
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |
考点:二倍角的正弦
专题:三角函数的求值
分析:根据函数f(x)=
sin2x,-1≤sin2x≤1,求得函数f(x)的最小值.
| 1 |
| 2 |
解答:
解:∵函数f(x)=sinxcosx=
sin2x,-1≤sin2x≤1,∴函数f(x)的最小值是-
,
故选:B.
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:本题主要考查二倍角公式、正弦函数的值域,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
执行如图所示的程序框图,则输出的结果是( )


| A、5 | B、7 | C、9 | D、11 |
已知方程
=k在(0,+∞)上有两个不同的解α,β(α<β),则下面结论正确的是( )
| |sinx| |
| x |
| A、sinα=αcosβ |
| B、sinα=-αcosβ |
| C、cosα=βsinβ |
| D、sinβ=-βsinα |
对于实数a和b,定义运算a*b,运算原理如图所示,则式子(
)-2*lne2的值为( )
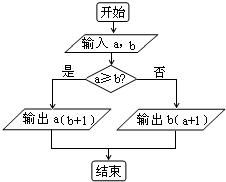
| 1 |
| 2 |

| A、8 | ||
| B、10 | ||
| C、12 | ||
D、
|
 (文科)如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
(文科)如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=