题目内容
 (文科)如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
(文科)如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=| 1 |
| 2 |
①面PAD⊥面PCD;
②AC与PB所成角的余弦值为
| ||
| 5 |
③面AMC与面BMC所成二面角的余弦值为-
| 2 |
| 3 |
考点:命题的真假判断与应用,异面直线及其所成的角,空间中直线与平面之间的位置关系,二面角的平面角及求法
专题:综合题,空间角,空间向量及应用
分析:由题设,①可由面面垂直的判定定理直接证明,得出结论是正确的;
②③根据题设可选择用空间向量法来做,建立如图的空间坐标系,即可判断出两者也是正确的
②③根据题设可选择用空间向量法来做,建立如图的空间坐标系,即可判断出两者也是正确的
解答:
解:①由题意,PA⊥底面ABCD,可得PA⊥CD,又四棱锥P-ABCD的底面为直角梯形,可得AD⊥CD,由线面垂直的判定定理可得CD⊥面PAD,再由面面垂直的判定定理可得面PAD⊥面PCD,故①正确;
②建立如图所示的坐标系,可得A(0,0,0),B(0,2,0),C(1,1,0),P(0,0,1),可得 :
:
=(1,1,0),
=(0,2,-1),故AC与PB所成角的余弦值为|
|=
,故②正确;
③在MC上取一点N(x,y,z),则存在实数λ使
=λ
,
=(1-x,1-y,y-z),
=(1,0,-
),
x=1-λ,y=1,z=
λ,要使AN⊥MC,只需
•
=0,即x-
z=0,解得λ=
,
可知,当λ=
时,N点的坐标为(
,-1,
),此时有
=(
,-1,
),
=(-
,1,-
),
此时有
•
=0,故可得AN,BN都与MC垂直,故∠ANB即为所求二面角的平面角,
又cos∠ANB=
=
=-
,故③正确
综上得①②③都正确
故答案为:①②③
②建立如图所示的坐标系,可得A(0,0,0),B(0,2,0),C(1,1,0),P(0,0,1),可得
 :
:| AC |
| PB |
| ||||
|
|
| ||
| 5 |
③在MC上取一点N(x,y,z),则存在实数λ使
| NC |
| MC |
| NC |
| MC |
| 1 |
| 2 |
x=1-λ,y=1,z=
| 1 |
| 2 |
| AN |
| MC |
| 1 |
| 2 |
| 4 |
| 5 |
可知,当λ=
| 4 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| AN |
| 1 |
| 5 |
| 2 |
| 5 |
| BN |
| 1 |
| 5 |
| 2 |
| 5 |
此时有
| AN |
| BN |
又cos∠ANB=
| ||||
| |AN||BN| |
-
| ||||||||||||
|
| 2 |
| 3 |
综上得①②③都正确
故答案为:①②③
点评:本题考查空间中面面垂直的判断,线线角与面面角的求法,是立体几何中综合性较强的题,运算难度大,由于本题的二面角的平面角用传统方法不易找出,利用空间向量解此类题比较有效

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
设函数f(x)=sinxcosx,x∈R,则函数f(x)的最小值是( )
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |
空间中,α,β,γ是三个互不重合的平面,l是一条直线,则下列命题中正确的是( )
| A、若α⊥β,l∥α,则l⊥β |
| B、若α⊥β,l⊥β,则l∥α |
| C、若l⊥α,l∥β,则α⊥β |
| D、若l∥α,l∥β,则α∥β |
在△ABC中,若AB=2,AC=3,∠A=60°,则BC的长为( )
A、
| ||
B、
| ||
| C、3 | ||
D、
|
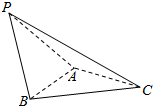 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.


 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为正三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为正三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.