题目内容
已知复数z=(m-1)(m+2)+(m-1)i(m∈R,i为虚数单位).
(1)若z为纯虚数,求m的值;
(2)若复数z在复平面内对应的点位于第四象限,求实数m的取值范围;
(3)若m=2,设
=a+bi(a,b∈R),求a+b.
(1)若z为纯虚数,求m的值;
(2)若复数z在复平面内对应的点位于第四象限,求实数m的取值范围;
(3)若m=2,设
| z+i |
| z-1 |
考点:复数的代数表示法及其几何意义
专题:计算题,数系的扩充和复数
分析:(1)由纯虚数的定义可得方程组,解出可得;
(2)由复数的几何意义可得
,解出即可;
(3)m=2,z=4+i,对等式右边化简由复数相等的条件可求a,b从而得答案;
(2)由复数的几何意义可得
|
(3)m=2,z=4+i,对等式右边化简由复数相等的条件可求a,b从而得答案;
解答:
解:(1)若z为纯虚数,则
,
解得m=-2;
(2)若复数z在复平面内对应的点位于第四象限,则
,
解得m<-2;
(3)若m=2,则z=4+i,
a+bi=
=
=
=
=
+
i,
∴a=
,b=
,
故a+b=
.
|
解得m=-2;
(2)若复数z在复平面内对应的点位于第四象限,则
|
解得m<-2;
(3)若m=2,则z=4+i,
a+bi=
| 4+i+i |
| 4+i-1 |
| 4+2i |
| 3+i |
| (4+2i)(3-i) |
| (3+i)(3-i) |
| 14+2i |
| 10 |
| 7 |
| 5 |
| 1 |
| 5 |
∴a=
| 7 |
| 5 |
| 1 |
| 5 |
故a+b=
| 8 |
| 5 |
点评:该题考查复数的有关概念、代数形式的运算及其几何意义,属基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
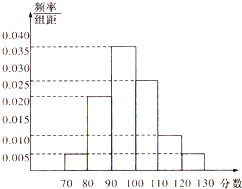 我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.
我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人. 一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.
一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.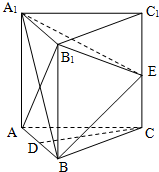 如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.