题目内容
若在由正整数构成的无穷数列{an}中,对任意的正整数n,都有an≤an+1,且对任意的正整数k,该数列中恰有2k-1个k,则a2014= .
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由对任意的正整数k,该数列中恰有2k-1个k,可知数列为:1,2,2,2,3,3,3,3,3,…
假设a2014在第n+1组中,由等差数列的求和公式求出前n组的和,解不等式n2<2014,得到n值后加1得答案.
假设a2014在第n+1组中,由等差数列的求和公式求出前n组的和,解不等式n2<2014,得到n值后加1得答案.
解答:
解:∵对任意的正整数k,该数列中恰有2k-1个k,
∴数列是1,2,2,2,3,3,3,3,3,…
设a2014在第n+1组中,则
1+3+5+…+(2n-1)=n2<2014,解得:n<45.
∴a2014在第45组中,
故a2014=45
故答案为:45.
∴数列是1,2,2,2,3,3,3,3,3,…
设a2014在第n+1组中,则
1+3+5+…+(2n-1)=n2<2014,解得:n<45.
∴a2014在第45组中,
故a2014=45
故答案为:45.
点评:本题考查数列递推式,解答的关键是对题意的理解,是中档题.

练习册系列答案
相关题目
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f(
),b=f(
),c=f(
),则( )
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、c<a<b |
设等差数列{an},{bn}的前n项和分别为Sn,Tn,且满足nTn=(n+4)Sn,则
的值为( )
| a8 |
| b9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
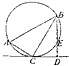 如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为
如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为