题目内容
已知抛物线y2=2px(p>0)的准线与圆x2+y2-2x-3=0相切,则p的值为 .
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由抛物线y2=2px(p>0)的准线与圆x2+y2-2x-3=0相切,知1+
=2,解得p=2.由此能求出抛物线方程.
| p |
| 2 |
解答:
解:圆x2+y2-2x-3=0转化为(x-1)2+y2=4,抛物线y2=2px(p>0)的准线为x=-
,
∵抛物线y2=2px(p>0)的准线与圆x2+y2-2x-3=0相切,
∴1+
=2,解得p=2.
故答案为:2.
| p |
| 2 |
∵抛物线y2=2px(p>0)的准线与圆x2+y2-2x-3=0相切,
∴1+
| p |
| 2 |
故答案为:2.
点评:本题考查抛物线的相关几何性质及直线与圆的位置关系等基础知识,考查运算求解能力,考查数形结合思想,注意应用直线与圆相切时圆心到直线的距离等于半径.

练习册系列答案
相关题目
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f(
),b=f(
),c=f(
),则( )
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、c<a<b |
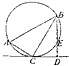 如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为
如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为