题目内容
11.不等式|x+1|≥kx对任意的x∈R均成立,则k的取值范围是( )| A. | (-∞,0) | B. | [-1,0] | C. | [0,1] | D. | [0,+∞) |
分析 由题意可得函数y=|x+1|的图象恒在直线y=kx的上方(含在直线y=kx上),数形结合可得k的范围.
解答  解:∵不等式|x+1|≥kx对任意的x∈R均成立,
解:∵不等式|x+1|≥kx对任意的x∈R均成立,
∴函数y=|x+1|的图象恒在直线y=kx的上方(含在直线y=kx上),
如图所示:
故有0≤k≤1,
故选:C.
点评 本题主要考查带有解绝对值的函数,函数的图象,函数的恒成立问题,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
2.(文)已知向量$\overrightarrow{a}$=(1,-1),$\overrightarrow{b}$=(1,1),$\overrightarrow{c}$=($\sqrt{2}$cosα,$\sqrt{2}$sinα)(a∈R),实数m,n满足m$\overrightarrow{a}$+n$\overrightarrow{b}$=2$\overrightarrow{c}$,则(m-4)2+n2的最大值为( )
| A. | 4 | B. | $20+8\sqrt{2}$ | C. | 32 | D. | 36 |
19.已知扇形的弧长是4cm,面积是2cm2,则扇形的圆心角的弧度数是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 1或4 |
16.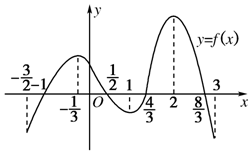 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )| A. | $[{-\frac{1}{3},1}]∪[2,3]$ | B. | $[{-1,\frac{1}{2}}]∪[{\frac{4}{3},\frac{8}{3}}]$ | ||
| C. | $[{-\frac{3}{2},\frac{1}{2}}]∪[1,2)$ | D. | $[{-\frac{3}{2},-\frac{1}{3}}]∪[{\frac{1}{2},\frac{4}{3}}]∪[{\frac{4}{3},3}]$ |
19.某中学进行高一学生体检,根据检查的学生每分钟脉搏数绘制了频率分布直方图(如图所示),根据频率分布直方图估计每分钟搏数在[69,85]的概率约为0.6.
| 组号 | 分组 | 频数 |
| 1 | [53,61) | 5 |
| 2 | [61,69) | 14 |
| 3 | [69,77) | 25 |
| 4 | [77,85) | 11 |
| 5 | [85,93) | 5 |
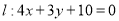 ,半径为
,半径为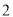 的圆
的圆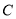 与
与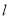 相切,圆心
相切,圆心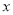 轴上且在直线
轴上且在直线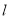 的右上方.
的右上方.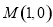 且与圆
且与圆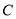 交于
交于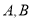 两点(
两点(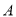 在
在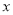 轴上方,B在
轴上方,B在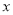 轴正半轴上是否存在定点
轴正半轴上是否存在定点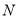 ,使得
,使得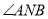 ?若存在,请求出点
?若存在,请求出点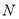 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.