题目内容
半径为R的球面上有A、B两点,它们的球面距离是
R,则线段AB的长为( )
| π |
| 2 |
A、
| ||||
| B、R | ||||
C、
| ||||
D、
|
考点:球面距离及相关计算
专题:计算题,球
分析:根据球面距离的概念得球心角,再在球的半径与弦AB构成的等腰直角三角形中求边长AB即可.
解答:
解:设球心为O,根据题意得:球心角为
,
∴在等腰直角三角形中求出斜边长为
R,
即得线段AB的长为
R,
故选:D.
| π |
| 2 |
∴在等腰直角三角形中求出斜边长为
| 2 |
即得线段AB的长为
| 2 |
故选:D.
点评:本题主要考查了球面距离以及解等腰直角三角形的能力,属于基础题.

练习册系列答案
相关题目
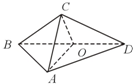 在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:
在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:①AC⊥BD;
②AD⊥CO;
③△AOC为正三角形;
④cos∠ADC=
| ||
| 4 |
⑤四面体ABCD的外接球面积为32π.
其中真命题是( )
| A、②③④ | B、①③④ |
| C、①④⑤ | D、①③⑤ |
执行如图的程序框图,如果输人的x为3,那么输出的结果是( )


| A、8 | B、6 | C、1 | D、-1 |
若函数f(x)=
(a∈R)是奇函数,则a的值为( )
| x+a |
| x2+1 |
| A、1 | B、0 | C、-1 | D、±1 |
某程序框图如图所示,若程序运行后,输出S的结果是( )


| A、246 | B、286 |
| C、329 | D、375 |
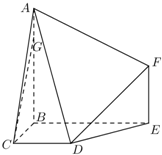 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.