题目内容
已知二次函数y=f(x)的定义域为R,f(1)=2,且在x=t,(t为实数)处取到最值,若y=g(x)为一次函数,且f(x)+g(x)=x2+2x-3.
(1)求y=f(x)的解析式(含t);
(2)若关于x的方程f(x)-g(x)=0在[2,4]上有解,求t的取值范围.
(1)求y=f(x)的解析式(含t);
(2)若关于x的方程f(x)-g(x)=0在[2,4]上有解,求t的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由对称轴x=t,设出f(x),再把f(1)=2代入求出即可,
(2)由(1)求出g(x)的表达式,将t用x表示出,由x的范围求出t的范围即可.
(2)由(1)求出g(x)的表达式,将t用x表示出,由x的范围求出t的范围即可.
解答:
解(1)设f(x)=x2-2tx+c,
由f(1)=2⇒c=2t+1,
∴f(x)=x2-2tx+2t+1.
(2)g(x)=x2+2x-3-f(x)
=(2+2t)x-(2t+4),
f(x)=g(x)
?x2-(4t+2)x+(4t+5)=0
?4t(x-1)=x2-2x+5
?t=
•
;
令k=x-1∈[1,3],
则t=
(k+
)∈[1,
],
故t的取值范围是[1,
].
由f(1)=2⇒c=2t+1,
∴f(x)=x2-2tx+2t+1.
(2)g(x)=x2+2x-3-f(x)
=(2+2t)x-(2t+4),
f(x)=g(x)
?x2-(4t+2)x+(4t+5)=0
?4t(x-1)=x2-2x+5
?t=
| 1 |
| 4 |
| (x-1)2+4 |
| (x-1) |
令k=x-1∈[1,3],
则t=
| 1 |
| 4 |
| 4 |
| k |
| 5 |
| 4 |
故t的取值范围是[1,
| 5 |
| 4 |
点评:本题考察了二次函数的性质,求二次函数的表达式,换元法,是一道中档题.

练习册系列答案
相关题目
已知随机变量Z服从正态分布N(0,σ2),若P(Z>1)=0.023,则P(-1≤Z≤1)=( )
| A、0.625 |
| B、0.954 |
| C、0.477 |
| D、0.977 |
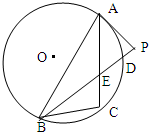 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.