题目内容
设f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β都是非零实数.若f(2010)=-1,求f(2011)的值.
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由条件求得 asinα+bsinβ=-1,再根据f(2011)=-(asinα+bsinβ ),从而求得结果.
解答:
解:∵f(x)=asin(πx+α)+bcos(πx+β),
f(2010)=-1=asin(2010π+α)+bcos(2010π+α)=asinα+bsinβ,
∴asinα+bsinβ=-1.
∴f(2011)=asin(2011π+α)+bcos(2011π+β)=-(asinα+bsinβ )=1.
f(2010)=-1=asin(2010π+α)+bcos(2010π+α)=asinα+bsinβ,
∴asinα+bsinβ=-1.
∴f(2011)=asin(2011π+α)+bcos(2011π+β)=-(asinα+bsinβ )=1.
点评:本题主要考查利用诱导公式进行化简求值,属于基础题.

练习册系列答案
相关题目
执行如图所示的程序框图,若输入x∈[0,π],则输出y的取值范围是( )


| A、[0,1] | ||||
B、[
| ||||
C、[-
| ||||
| D、[-1,1] |
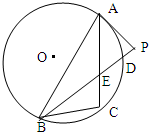 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.