题目内容

已知向量
a
=（3，4），
b
=（-2，1），若（
a
+x
b
）⊥
b
，则实数x为（　　）
A、-
1
5
B、-
2
5
C、
1
5
D、
2
5
考点：平面向量数量积的运算,平面向量的坐标运算
专题：平面向量及应用
分析：求出
a
+x
b
的坐标，利用垂直关系得到向量的数量积为0，即可求出x的值．
解答： 解：∵向量
a
=（3，4），
b
=（-2，1），
∴
a
+x
b
=（3-2x，4+x），
（
a
+x
b
）⊥
b
，∴-6+4x+4+x=0
解得x=
2
5
．
故选：D．
点评：本题考查向量的垂直条件的应用，向量的坐标运算，考查计算能力．
练习册系列答案
相关题目
如图所示，在边长为2的正六边形ABCDEF中，动圆Q的半径为1，圆心在线段CD（含端点）上运动，P是圆Q上及内部的动点，设向量
AP
=m
AB
+n
AF
（m、n为实数），则m+n的最大值为
 
．
A是曲线C1：
x2
9
+
y2
4
=1与C2：
x2
4
-y2=1的一个交点，且A到C1的两焦点的距离之和为m，到C2两焦点距离之差的绝对值为n，则lg（m+n）=
 
．
某所学校计划招聘男教师x名，女教师y名，x和y须满足约束条件
2x-y≥5
x-y≤2
x≤5
，则该校招聘的教师最多是
 
名．
半径为R的球的内接正三棱柱的三个侧面积之和的最大值为（　　）
A、3
3
R2
B、
3
R2
C、2
2
R2
D、
2
R2
已知F1、F2是离心率为
2
的双曲线C的左、右焦点，点P在C上，若|PF1|=2|PF2|，则cos∠F1PF2=（　　）
A、
4
5
B、
3
4
C、
3
5
D、
1
4
已知函数f（x）=
1
2x
-cosx，若
π
3
＜a＜b＜
5π
6
，则（　　）
A、f（a）＞f（b）
B、f（a）＜f（b）
C、f（a）=f（b）
D、f（a）f（b）＞0
四个小动物换座位，开始是鼠、猴、兔、猫分别坐1、2、3、4号位上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，…这样交替进行下去，那么第2014次互换座位后，小兔坐在第（　　）号座位上．
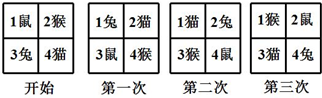
A、1B、2C、3D、4
若θ为三角形一个内角，且对任意实数x，x2cosθ-4xsinθ+6＞0恒成立，则θ的取值范围为（　　）
A、（
π
3
，
π
2
）
B、（0，
π
6
）
C、（0，
π
3
）
D、（
π
6
，π）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网