题目内容
 如图所示,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图所示,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:连接AE会发现它与AB垂直,所以构造
•
,将条件中的
=m
+n
带人,便会得到
•
=m
•
+n
•
,而
•
=0,所以经过化简就可得到
•
=6n.同样的办法你会得到
•
=6m,显然得到的这两式需相加便经过化简得到m+n=|
|cos∠PAO,而这正好是
在
方向上的投影,所以求这个投影的最大值即可,而投影的最大值,通过图形就能得到.
| AP |
| AE |
| AP |
| AB |
| AF |
| AP |
| AE |
| AB |
| AE |
| AF |
| AE |
| AB |
| AE |
| AP |
| AE |
| AP |
| AC |
| AP |
| AP |
| AO |
解答:
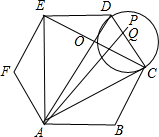 解:如图所示,
解:如图所示,
=m
+n
.
∴
•
=m
•
+n
•
=n
•
=n|
||
|cos∠FAE=6n ①
同理,
•
=6m ②
①+②得:
•(
+
)=6(m+n);
∵
+
=2
,∴2
•
=6(m+n).
∵
•
=|
||
|cos∠PAO=3|
|cos∠PAO.
∴m+n=|
|cos∠PAO,其几何意义就是
在
上的投影.
∴求m+n的最大值就转化为求
在
上投影最大值.
从图形上可以看出:当点Q和D点重合时,
在
上的投影取到最大值5.
 解:如图所示,
解:如图所示,| AP |
| AB |
| AF |
∴
| AP |
| AE |
| AB |
| AE |
| AF |
| AE |
| AF |
| AE |
| AF |
| AE |
同理,
| AP |
| AC |
①+②得:
| AP |
| AE |
| AC |
∵
| AE |
| AC |
| AO |
| AP |
| AO |
∵
| AP |
| AO |
| AP |
| AO |
| AP |
∴m+n=|
| AP |
| AP |
| AO |
∴求m+n的最大值就转化为求
| AP |
| AO |
从图形上可以看出:当点Q和D点重合时,
| AP |
| AO |
点评:本题需注意的是构造两组数量级,将求m+n的最大值转化为求
在
方向上投影的最大值.
| AP |
| AO |

练习册系列答案
相关题目
已知向量
=(3,4),
=(-2,1),若(
+x
)⊥
,则实数x为( )
| a |
| b |
| a |
| b |
| b |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
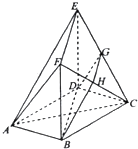 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE,CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE,CF的中点.