题目内容
6.设函数f(x)=|x-a|,a∈R.(Ⅰ)当a=2时,解不等式:f(x)≥6-|2x-5|;
(Ⅱ)若关于x的不等式f(x)≤4的解集为[-1,7],且两正数s和t满足2s+t=a,求证:$\frac{1}{s}+\frac{8}{t}≥6$.
分析 (Ⅰ)利用绝对值的意义表示成分段函数形式,解不等式即可.
(2)根据不等式的解集求出a=3,利用1的代换结合基本不等式进行证明即可.
解答 (Ⅰ)解:当a=2时,不等式:f(x)≥6-|2x-5|,可化为|x-2|+|2x-5|≥6.
①x≥2.5时,不等式可化为x-2+2x-5≥6,∴x≥$\frac{13}{3}$;
②2≤x<2.5,不等式可化为x-2+5-2x≥6,∴x∈∅;
③x<2,不等式可化为2-x+5-2x≥6,∴x≤$\frac{1}{3}$,
综上所述,不等式的解集为(-$∞,\frac{1}{3}$]$∪[\frac{13}{3},+∞)$;
(Ⅱ)证明:不等式f(x)≤4的解集为[a-4,a+4]=[-1,7],∴a=3,
∴$\frac{1}{s}+\frac{8}{t}$=$\frac{1}{3}$($\frac{1}{s}+\frac{8}{t}$)(2s+t)=$\frac{1}{3}$(10+$\frac{t}{s}$+$\frac{16s}{t}$)≥6,当且仅当s=$\frac{1}{2}$,t=2时取等号.
点评 本题主要考查不等式的求解和应用,根据绝对值不等式的性质转化为分段函数形式,利用1的代换转化为基本不等式是解决本题的关键.综合性较强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.复数$z=\frac{10i}{3+i}$(i为虚数单位)的虚部为( )
| A. | 1 | B. | 3 | C. | -3 | D. | $\frac{15}{4}$ |
18.中石化集团通过与安哥拉国家石油公司合作,获得了安哥拉深海油田区块的开采权,集团在某些区块随机初步勘探了部分口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井.以节约勘探费用.勘探初期数据资料见如表:
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为y=6.5x+a,求a,并估计y的预报值;
(2)设出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有的出油量不低于50L的井中任意勘察3口井,求恰有2口是优质井的概率.
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(2)设出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有的出油量不低于50L的井中任意勘察3口井,求恰有2口是优质井的概率.
15.已知P、Q分别在射线y=x(x>0)和y=-x(x>0)上,且△POQ的面积为1,(0为原点),则线段PQ中点M的轨迹为( )
| A. | 双曲线x2-y2=1 | B. | 双曲线x2-y2=1的右支 | ||
| C. | 半圆x2+y2=1(x<0) | D. | 一段圆弧x2+y2=1(x>$\frac{{\sqrt{2}}}{2}$) |
 如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.
如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.


 △ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{{\sqrt{3}sinC}}{cosB}=\frac{c}{b}$.
△ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{{\sqrt{3}sinC}}{cosB}=\frac{c}{b}$.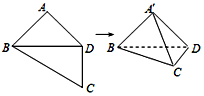 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).