题目内容
已知点P是直线l:3x-4y+5=0上的动点,定点Q的坐标为(1,1),求线段PQ长的最小值及取得最小值时P的坐标.
考点:两点间距离公式的应用
专题:计算题,直线与圆
分析:线段PQ长的最小值为Q到直线l:3x-4y+5=0的距离,PQ:4x+3y-7=0,与直线l:3x-4y+5=0联立可得P的坐标.
解答:
解:线段PQ长的最小值为Q到直线l:3x-4y+5=0的距离,即d=
=
,
此时PQ:4x+3y-7=0,
与直线l:3x-4y+5=0联立可得P(
,
).
| |3-4+5| |
| 5 |
| 4 |
| 5 |
此时PQ:4x+3y-7=0,
与直线l:3x-4y+5=0联立可得P(
| 13 |
| 25 |
| 41 |
| 25 |
点评:本题考查两点间距离公式的应用,考查学生的计算能力,比较基础.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
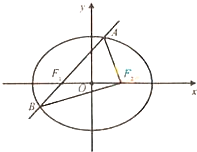 如图,椭圆E:
如图,椭圆E: