题目内容
已知数列{an}的前n项和为Sn=n2+2n+3.
(1)求数列{an}的通项公式;
(2)求数列{Sn}前5项和.
(1)求数列{an}的通项公式;
(2)求数列{Sn}前5项和.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)当n=1时代入Sn=n2+2n+3求出a1的值,当n>2时,由an=Sn-Sn-1求出an的表达式,再验证a1的值,最后写出an的通项公式;
(2)根据Sn=n2+2n+3的特点,利用分组求和法求出数列{Sn}前5项和.
(2)根据Sn=n2+2n+3的特点,利用分组求和法求出数列{Sn}前5项和.
解答:
解:(1)因为数列{an}的前n项和Sn=n2+2n+3,
所以当n≥2时,
an=Sn-Sn-1=n2+2n+3-[(n-1)2+2(n-1)+3]=2n+7,
又当n=1时,a1=S1=6≠2×1+7,
所以an=
,
(2)设数列{Sn}前5项和为S,
则S=(12+22+32+42+52)+2(1+2+3+4+5)+5×3
=55+30+15=100.
所以当n≥2时,
an=Sn-Sn-1=n2+2n+3-[(n-1)2+2(n-1)+3]=2n+7,
又当n=1时,a1=S1=6≠2×1+7,
所以an=
|
|
(2)设数列{Sn}前5项和为S,
则S=(12+22+32+42+52)+2(1+2+3+4+5)+5×3
=55+30+15=100.
点评:本题考查利用an=Sn-Sn-1(n≥2)求数列的通项公式,注意验证n=1时是否成立,及数列求和的方法:分组求和法.

练习册系列答案
相关题目
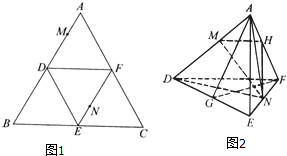 如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2.
如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2. 如图,甲、乙两塔相距120m,在甲塔点A测得乙塔顶的仰角为α,在乙塔点C测得甲塔塔顶的仰角为2α,在两塔间正中一点M测得两塔塔顶的仰角互余,求甲、乙两塔的高度.
如图,甲、乙两塔相距120m,在甲塔点A测得乙塔顶的仰角为α,在乙塔点C测得甲塔塔顶的仰角为2α,在两塔间正中一点M测得两塔塔顶的仰角互余,求甲、乙两塔的高度.