题目内容
已知正实数a、b满足:a2+b2=2
.
(1)求
+
的最小值m;
(2)设函数f(x)=|x-t|+|x+
|(t≠0),对于(1)中求得的m,是否存在实数x,使得f(x)=
成立,说明理由.
| ab |
(1)求
| 1 |
| a |
| 1 |
| b |
(2)设函数f(x)=|x-t|+|x+
| 1 |
| t |
| m |
| 2 |
考点:基本不等式
专题:不等式的解法及应用
分析:(1)利用基本不等式的性质即可得出;
(2)利用绝对值形式的三角不等式的性质即可得出.
(2)利用绝对值形式的三角不等式的性质即可得出.
解答:
解:(1)∵2
=a2+b2≥2ab,即
≥ab,∴
≤1.
又∴
+
≥
≥2,当且仅当a=b时取等号.
∴m=2.
(2)函数f(x)=|x-t|+|x+
|≥|t+
|≥2>
=1,
∴满足条件的实数x不存在.
| ab |
| ab |
| ab |
又∴
| 1 |
| a |
| 1 |
| b |
| 2 | ||
|
∴m=2.
(2)函数f(x)=|x-t|+|x+
| 1 |
| t |
| 1 |
| t |
| 2 |
| 2 |
∴满足条件的实数x不存在.
点评:本题考查了基本不等式的性质、绝对值形式的三角不等式的性质,考查了计算能力,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
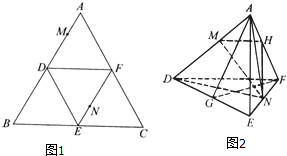 如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2.
如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2. 如图,甲、乙两塔相距120m,在甲塔点A测得乙塔顶的仰角为α,在乙塔点C测得甲塔塔顶的仰角为2α,在两塔间正中一点M测得两塔塔顶的仰角互余,求甲、乙两塔的高度.
如图,甲、乙两塔相距120m,在甲塔点A测得乙塔顶的仰角为α,在乙塔点C测得甲塔塔顶的仰角为2α,在两塔间正中一点M测得两塔塔顶的仰角互余,求甲、乙两塔的高度.