题目内容
4.已知F1,F2为平面内两定点,|F1F2|=6,动点M满足||MF1|-|MF2||=6,则M的轨迹是( )| A. | 两条射线 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
分析 可作出线段F1F2和点M,判断M点的位置:分成点M不在线段F1F2所在直线上,点M在线段F1F2(不含端点)上,以及点M在线段F1F2的延长线或反向延长线上这几种情况,结合图形及三角形两边之差和第三边的关系便可找出点M的位置,从而找出点M的轨迹.
解答 解:(1)如图,M点不在线段F1F2所在直线上或在线段F1F2上(不含端点)时,显然||MF1|-|MF2||<|F1F2|,不满足条件;
(2)当M点在线段F1F2的延长线或反向延长线上时,满足||MF1|-|MF2||=|F1F2|;
∴M的轨迹为两条射线.
故选A.
点评 考查分类讨论的思想,以及数形结合的解题方法,三角形的两边之差和第三边的关系.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14.已知函数f(x)=|ln(x-1)|,若实数a,b(a<b)满足f(a)=f(b),则-a+5b的取值范围为( )
| A. | (5,8) | B. | (8,9) | C. | (5,9) | D. | (8,+∞) |
12.图1是某学生的数学考试成绩的茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14,图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图,那么程序框图输出的结果是( )
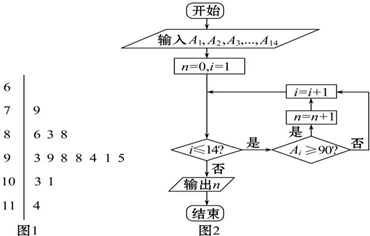

| A. | 14 | B. | 9 | C. | 10 | D. | 7 |
19.过点P(2,1)且在x,y轴上的截距相等的直线方程为( )
| A. | x-2y=0 | B. | 2x-y=0或x+y-3=0 | C. | x+y-3=0 | D. | x-2y=0或x+y-3=0 |
15.若函数f(x)=$\left\{\begin{array}{l}{ax+a,x≤0}\\{xlnx,x>0}\end{array}\right.$ 的图象上有且仅有两对点关于原点对称,则a的取值范围是( )
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{e}$)∪(1,e) | C. | (1,+∞) | D. | (0,1)∪(1,+∞) |
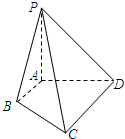 如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.
如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.