题目内容
5.某手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如表:女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | |||
| “不认可”手机 | |||
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
分析 (Ⅰ)利用数据直接填写联列表即可,求出X2,即可回答是否有95%的把握认为性别和对手机的“认可”有关;
(Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于8(0分)有6人,其中评分小于9(0分)的人数为4,从6人人任取3人,记评分小于9(0分)的人数为X,则X取值为1,2,3,求出相应概率,得到X的分布列,然后求解期望.
解答 解:(Ⅰ)2×2列联表如下图:
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
${Χ^2}=\frac{{500{{(140×120-180×60)}^2}}}{200×300×320×180}≈5.208>3.841$,
所以有95%的把握认为性别和对手机的“认可”有关.…(6分)
(Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于8(0分)有6人,其中评分小于9(0分)的人数为4,从6人人任取3人,记评分小于9(0分)的人数为X,则X取值为1,2,3,$P(X=1)=\frac{C_4^1C_2^2}{C_6^3}=\frac{4}{20}=\frac{1}{5}$;$P(X=2)=\frac{C_4^2C_2^1}{C_6^3}=\frac{12}{20}=\frac{3}{5}$;$P(X=3)=\frac{C_4^3C_2^2}{C_6^3}=\frac{4}{20}=\frac{1}{5}$.
…(9分)
所以X的分布列为
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查独立检验以及离散性随机变量的分布列以及期望的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
20.经过1小时,时针旋转的角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
14.已知函数f(x)=|ln(x-1)|,若实数a,b(a<b)满足f(a)=f(b),则-a+5b的取值范围为( )
| A. | (5,8) | B. | (8,9) | C. | (5,9) | D. | (8,+∞) |
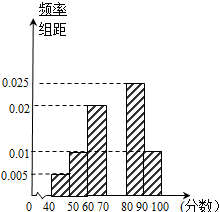 某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.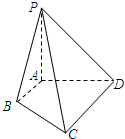 如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.
如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.