题目内容
3.已知抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)在抛物线上,直线l与抛物线y2=4x相交于不同的A、B两点(1)求该抛物线方程;
(2)若直线l过抛物线的焦点,且线段AB中点的横坐标为2,求弦AB的长;
(3)若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-4,证明直线l必过一定点,并求出该定点.
分析 (1)设抛物线的方程为:y2=2px,利用点P(1,2)在抛物线上,求出p,即可求出抛物线的方程;
(2)由于直线过焦点,先利用中点的坐标公式求出x1+x2,利用弦长公式x1+x2+p求出AB的长;
(3)设l:x=ty+b代入抛物线方程y2=4x,消去x得y2-4ty-4b=0,利用韦达定理,结合$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=-4,即可证明结论.
解答 解:(1)设抛物线的方程为:y2=2px,
∵点P(1,2)在抛物线上,
∴4=2p,
∴p=2,
∴抛物线方程为y2=4x;
(2)设A、B两点横坐标分别为x1,x2,
因为线段AB中点的横坐标为2,
所以x1+x2=4,
故|AB|=x1+x2+p=4+2=6.
证明:(3)设l:x=ty+b代入抛物线方程y2=4x,消去x得
y2-4ty-4b=0,设A(x1,y1),B(x2,y2),
则y1+y2=4t,y1y2=-4b,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2
=(ty1+b)(ty2+b)+y1y2
=t2y1y2+bt(y1+y2)+b2+y1y2
=-4bt2+4bt2+b2-4b=b2-4b.
令b2-4b=-4,
∴b2-4b+4=0,
∴b=2,
∴直线l过定点(2,0).
∴若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-4,则直线l必过一定点.
点评 本题考查抛物线的方程,考查弦长问题,考查直线与抛物线的位置关系,考查学生的计算能力.对于过焦点的弦长注意圆锥曲线定义的应用.

练习册系列答案
相关题目
14.已知函数f(x)=|ln(x-1)|,若实数a,b(a<b)满足f(a)=f(b),则-a+5b的取值范围为( )
| A. | (5,8) | B. | (8,9) | C. | (5,9) | D. | (8,+∞) |
18.命题“?x∈R,cosx<$\frac{1}{2}$”的否定是( )
| A. | ?x<R,cosx≥$\frac{1}{2}$ | B. | ?x∈R,cosx>$\frac{1}{2}$ | C. | ?x<R,cosx≥$\frac{1}{2}$ | D. | ?x∈R,cosx>$\frac{1}{2}$ |
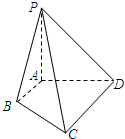 如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.
如图,已知PA⊥平面ABCD,PA=AB=AD=$\frac{1}{2}$CD=1,∠BAD=∠ADC=90°.