题目内容
2.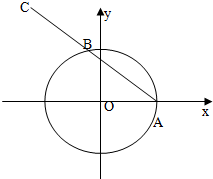 如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.
如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.(1)若点C在y轴的正半轴上,求$\overrightarrow{OA}$•$\overrightarrow{OB}$;
(2)若∠AOB=$\frac{2π}{3}$,求点A到直线OC的距离.
分析 (1)由点C在y轴正半轴上,可得xC=0,又点B是线段AC的中点,利用中点坐标公式可得xB,即可得出$\overrightarrow{OA}$•$\overrightarrow{OB}$.
(2)由$∠AOB=\frac{2π}{3}$,可得$B(-\frac{1}{2},\frac{{\sqrt{3}}}{2})$,利用中点坐标公式可得:C坐标,可得直线OC的方程,利用点A到直线OC的距离公式即可得出.
解答 解:(1)∵点C在y轴正半轴上,
∴xC=0,又点B是线段AC的中点,
∴xA+xC=2xB,∴${x_B}=\frac{1}{2}$,
∴$\overrightarrow{OA}•\overrightarrow{OB}=\frac{1}{2}$.
(2)∵$∠AOB=\frac{2π}{3}$,∴$B(-\frac{1}{2},\frac{{\sqrt{3}}}{2})$,
由点B是线段AC的中点,∴$C(-2,\sqrt{3})$,
∴直线OC的方程为$y=-\frac{{\sqrt{3}}}{2}x$,即$\sqrt{3}x+2y=0$,
∴点A到直线OC的距离$d=\frac{{|{\sqrt{3}}|}}{{\sqrt{3+4}}}=\frac{{\sqrt{21}}}{7}$.
点评 本题考查了中点坐标公式、直线方程、单位圆、点到直线距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知函数f(x)=|ln(x-1)|,若实数a,b(a<b)满足f(a)=f(b),则-a+5b的取值范围为( )
| A. | (5,8) | B. | (8,9) | C. | (5,9) | D. | (8,+∞) |
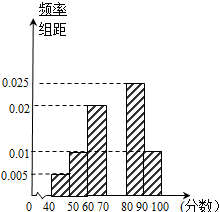 某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.