题目内容
已知函数f(x)=ae2x-be-2x-cx(a,b,c∈R)的导函数f′(x)为偶函数,且曲线y=f(x)在点(0,f(0))处的切线斜率为4-c,若f(x)有极值,则c的取值范围是( )
| A、(2,+∞) |
| B、[2,+∞) |
| C、[4,+∞) |
| D、(4,+∞) |
考点:利用导数研究曲线上某点切线方程,导数的运算
专题:综合题,导数的综合应用
分析:根据函数f(x)=ae2x-be-2x-cx(a,b,c∈R)的导函数f′(x)为偶函数,且曲线y=f(x)在点(0,f(0))处的切线的斜率为4-c,构造关于a,b的方程,可得a,b的值,结合基本不等式,分c≤4时和c>4时两种情况讨论f(x)极值的存在性,最后综合讨论结果,可得答案.
解答:
解:∵函数f(x)=ae2x-be-2x-cx(a,b,c∈R)
∴f′(x)=2ae2x+2be-2x-c,
由f′(x)为偶函数,可得2(a-b)(e2x-e-2x)=0,
即a=b,
又∵曲线y=f(x)在点(0,f(0))处的切线的斜率为4-c,
即f′(0)=2a+2b-c=4-c,故a=b=1,
∴f′(x)=2e2x+2e-2x-c,
而2e2x+2e-2x≥2
=4,当且仅当x=0时取等号,
当c≤4时,f′(x)≥0恒成立,故f(x)无极值;
当c>4时,令t=e2x,方程2t+
-c=0的两根均为正,即f′(x)=0有两个根x1,x2,
当x∈(x1,x2)时,f′(x)<0,当x∈(-∞x1)∪(x2,+∞)时,f′(x)>0,
故当x=x1,或x=x2时,f(x)有极值,
综上,若f(x)有极值,c的取值范围为(4,+∞).
故选:D.
∴f′(x)=2ae2x+2be-2x-c,
由f′(x)为偶函数,可得2(a-b)(e2x-e-2x)=0,
即a=b,
又∵曲线y=f(x)在点(0,f(0))处的切线的斜率为4-c,
即f′(0)=2a+2b-c=4-c,故a=b=1,
∴f′(x)=2e2x+2e-2x-c,
而2e2x+2e-2x≥2
| 2e2x•2e-2x |
当c≤4时,f′(x)≥0恒成立,故f(x)无极值;
当c>4时,令t=e2x,方程2t+
| 2 |
| t |
当x∈(x1,x2)时,f′(x)<0,当x∈(-∞x1)∪(x2,+∞)时,f′(x)>0,
故当x=x1,或x=x2时,f(x)有极值,
综上,若f(x)有极值,c的取值范围为(4,+∞).
故选:D.
点评:本题考查的知识点是利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,是导数的综合应用,难度中档.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为
如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为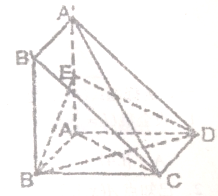 四边形ABCD与A′ABB′都是边长为a的正方形,且平面ABB′A′⊥平面ABCD,点E是A′A的中心.
四边形ABCD与A′ABB′都是边长为a的正方形,且平面ABB′A′⊥平面ABCD,点E是A′A的中心.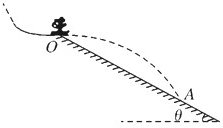 如图,跳台滑雪运动员(可视为质点)经过一段加速滑行后从O点水平飞出,落到斜坡上的A点,已知O点是斜坡的起点,测得A点与O点距离L=12m,斜坡与水平的夹角θ=37°,运动员的质量m=50kg,不计空气阻力,取sin37°=0.60,cos37°=0.80,g取10m/s2.求:
如图,跳台滑雪运动员(可视为质点)经过一段加速滑行后从O点水平飞出,落到斜坡上的A点,已知O点是斜坡的起点,测得A点与O点距离L=12m,斜坡与水平的夹角θ=37°,运动员的质量m=50kg,不计空气阻力,取sin37°=0.60,cos37°=0.80,g取10m/s2.求: