题目内容
 如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为
如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为| 2 |
(1)求证:AC⊥SD;
(2)F为SD的中点,若SD⊥平面PAC,求证:BF∥平面PAC.
考点:直线与平面垂直的性质,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)连接SO,可证SO⊥AC,又SO∩BD=O,可证明AC⊥平面SBD,又SD?平面SBD,即可证明AC⊥SD.
(Ⅱ)连接OP,可证OP⊥SD,又△SBD中,BD=
a=SB,且F为SD中点,可证BF⊥SD,由OP,BF?平面BDF,可证OP∥BF,又OP?平面ACP,BD?平面ACP,BF?平面PAC,即可证明BF∥平面PAC.
(Ⅱ)连接OP,可证OP⊥SD,又△SBD中,BD=
| 2 |
解答:
 证明:(Ⅰ)连接SO,
证明:(Ⅰ)连接SO,
∵四边形ABCD为正方形,
∴AC⊥BD且O为AC中点,
又∵SA=SC
∴SO⊥AC
又∵SO∩BD=O,
∴AC⊥平面SBD,(5分)
又∵SD?平面SBD,
∴AC⊥SD.(7分)
(Ⅱ)连接OP,
∵SD⊥平面ACP,OP?平面ACP,
∴OP⊥SD,(9分)
又△SBD中,BD=
a=SB,且F为SD中点,∴BF⊥SD,
因为OP,BF?平面BDF,所以OP∥BF,(11分)
又∵OP?平面ACP,BD?平面ACP,BF?平面PAC,
∴BF∥平面PAC.(13分)
 证明:(Ⅰ)连接SO,
证明:(Ⅰ)连接SO,∵四边形ABCD为正方形,
∴AC⊥BD且O为AC中点,
又∵SA=SC
∴SO⊥AC
又∵SO∩BD=O,
∴AC⊥平面SBD,(5分)
又∵SD?平面SBD,
∴AC⊥SD.(7分)
(Ⅱ)连接OP,
∵SD⊥平面ACP,OP?平面ACP,
∴OP⊥SD,(9分)
又△SBD中,BD=
| 2 |
因为OP,BF?平面BDF,所以OP∥BF,(11分)
又∵OP?平面ACP,BD?平面ACP,BF?平面PAC,
∴BF∥平面PAC.(13分)
点评:本题主要考查了直线与平面平行的判定,以及直线与平面垂直的性质,涉及到的知识点比较多,知识性技巧性都很强,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知函数f(x)=ae2x-be-2x-cx(a,b,c∈R)的导函数f′(x)为偶函数,且曲线y=f(x)在点(0,f(0))处的切线斜率为4-c,若f(x)有极值,则c的取值范围是( )
| A、(2,+∞) |
| B、[2,+∞) |
| C、[4,+∞) |
| D、(4,+∞) |
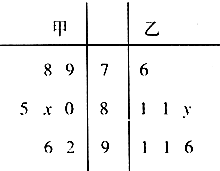 某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.