题目内容
正三棱柱ABC-A1B1C1的棱长均为a,D、E分别为C1C与AB的中点,A1B交AB1于点G.
(1)求证:A1B⊥AD;
(2)求证:CE∥平面AB1D.
(1)求证:A1B⊥AD;
(2)求证:CE∥平面AB1D.
考点:直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)连接A1D,BD,由A1ABB1为正方形,得A1B⊥AB1,A1D=BD,从而A1B⊥DG,进而A1B⊥平面AB1D,由此能证明A1B⊥AD.
(2)连接GE,GD,则GE⊥平面ABC,GE∥DC,四边形GECD为平行四边形,由此能证明EC∥平面AB1D.
(2)连接GE,GD,则GE⊥平面ABC,GE∥DC,四边形GECD为平行四边形,由此能证明EC∥平面AB1D.
解答:
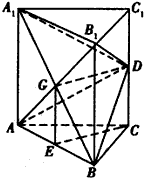 证明:(1)连接A1D,BD,
证明:(1)连接A1D,BD,
∵三棱柱ABC-A1B1C1是棱长均为a的正三棱柱,
∴A1ABB1为正方形,∴A1B⊥AB1,
∵D是C1C的中点,∴△A1C1D≌△BCD,∴A1D=BD,
∵G是A1B中点,∴A1B⊥DG,
又∵DG∩AB1=G,∴A1B⊥平面AB1D,
又∵AD?平面AB1D,∴A1B⊥AD.
(2)连接GE,GD,∵EG∥A1A,∴GE⊥平面ABC,
∵DC⊥平面ABC,∴GE∥DC,
∵GE=DC=
a,
∴四边形GECD为平行四边形,
∴EC∥GD,
又∵EC?平面AB1D,DG?平面AB1D,
∴EC∥平面AB1D.
 证明:(1)连接A1D,BD,
证明:(1)连接A1D,BD,∵三棱柱ABC-A1B1C1是棱长均为a的正三棱柱,
∴A1ABB1为正方形,∴A1B⊥AB1,
∵D是C1C的中点,∴△A1C1D≌△BCD,∴A1D=BD,
∵G是A1B中点,∴A1B⊥DG,
又∵DG∩AB1=G,∴A1B⊥平面AB1D,
又∵AD?平面AB1D,∴A1B⊥AD.
(2)连接GE,GD,∵EG∥A1A,∴GE⊥平面ABC,
∵DC⊥平面ABC,∴GE∥DC,
∵GE=DC=
| 1 |
| 2 |
∴四边形GECD为平行四边形,
∴EC∥GD,
又∵EC?平面AB1D,DG?平面AB1D,
∴EC∥平面AB1D.
点评:本小题主要线线垂直、线面平行、探索性问题等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若a、b是函数f(x)=|log3x|-3-x的两个零点,则( )
| A、0<ab<1 |
| B、ab=1 |
| C、1<ab<2 |
| D、ab≥2 |
已知函数f(x)=ae2x-be-2x-cx(a,b,c∈R)的导函数f′(x)为偶函数,且曲线y=f(x)在点(0,f(0))处的切线斜率为4-c,若f(x)有极值,则c的取值范围是( )
| A、(2,+∞) |
| B、[2,+∞) |
| C、[4,+∞) |
| D、(4,+∞) |