题目内容
二面角的棱与这个二面角的平面角所在的平面的关系是 ．
考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：由二面角的棱与二面角的平面角的定义，作出图，根据直线与平面垂直的判定定理即可得解．
解答：
解：平面内的一条直线把平面分为两部分，其中的每一部分都叫做半平面，从一条直线出发的两个半平面所组成的图形，叫做二面角（这条直线叫做二面角的棱，每个半平面叫做二面角的面）．
以二面角的公共直线上任意一点为端点，在两个面内分别作垂直于公共直线的两条射线，这两条射线所成的角叫做二面角的平面角．
如图，由以上定义可知：
若∠AOB是平面α和β的平面角，
则l⊥OA，l⊥OB，
∴l⊥平面OAB
故答案为：相交且垂直．
解：平面内的一条直线把平面分为两部分，其中的每一部分都叫做半平面，从一条直线出发的两个半平面所组成的图形，叫做二面角（这条直线叫做二面角的棱，每个半平面叫做二面角的面）．以二面角的公共直线上任意一点为端点，在两个面内分别作垂直于公共直线的两条射线，这两条射线所成的角叫做二面角的平面角．
如图，由以上定义可知：
若∠AOB是平面α和β的平面角，
则l⊥OA，l⊥OB，
∴l⊥平面OAB
故答案为：相交且垂直．
点评：本题主要考查了直线与平面垂直的判定，考查了二面角的棱与二面角的平面角的定义，属于基本知识的考查．
练习册系列答案
相关题目
若a、b是函数f（x）=|log3x|-3-x的两个零点，则（ ）
| A、0＜ab＜1 |
| B、ab=1 |
| C、1＜ab＜2 |
| D、ab≥2 |
已知函数f（x）=ae2x-be-2x-cx（a，b，c∈R）的导函数f′（x）为偶函数，且曲线y=f（x）在点（0，f（0））处的切线斜率为4-c，若f（x）有极值，则c的取值范围是（ ）
| A、（2，+∞） |
| B、[2，+∞） |
| C、[4，+∞） |
| D、（4，+∞） |
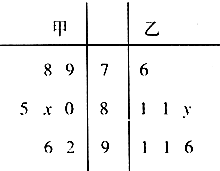某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83．