题目内容
求函数y=log0.5（3+2x-x2）的单调区间．
考点：复合函数的单调性
专题：函数的性质及应用
分析：令t=3+2x-x2 ＞0，求得函数的定义域为（-1，3），且y=log0.5 t．求得t在定义域内的增区间，即为函数y的减区间；求得t在定义域内的减区间，即为函数y的增区间．
解答：
解：令t=3+2x-x2 ＞0，求得-1＜x＜3，可得函数的定义域为（-1，3），且y=log0.5 t，
求得t=3+2x-x2 在定义域内的增区间为（-1，1]，可得函数y的减区间为（-1，1]；
求得t=3+2x-x2 在定义域内的减区间为[1，3），可得函数y的增区间为[1，3）．
求得t=3+2x-x2 在定义域内的增区间为（-1，1]，可得函数y的减区间为（-1，1]；
求得t=3+2x-x2 在定义域内的减区间为[1，3），可得函数y的增区间为[1，3）．
点评：本题主要考查复合函数的单调性，对数函数、二次函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=ae2x-be-2x-cx（a，b，c∈R）的导函数f′（x）为偶函数，且曲线y=f（x）在点（0，f（0））处的切线斜率为4-c，若f（x）有极值，则c的取值范围是（ ）
| A、（2，+∞） |
| B、[2，+∞） |
| C、[4，+∞） |
| D、（4，+∞） |
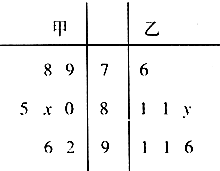某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83．
如图，AD、BE是△ABC的两条高，求证：∠CED=∠ABC．