题目内容
若正数a,b满足
+
=1,则
+
的最小值为 .
| 1 |
| a |
| 1 |
| b |
| 4 |
| a-1 |
| 16 |
| b-1 |
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:由条件可得,
=
,且
=
,代入所求式子,再由基本不等式,即可得到最小值,注意等号成立的条件.
| 1 |
| b-1 |
| a |
| b |
| 1 |
| a-1 |
| b |
| a |
解答:
解:正数a,b满足
+
=1,
则有
=1-
=
,
则有
=
,
=1-
=
,即有
=
,
则有
+
=
+
≥2
=16,
当且仅当
=
即有b=2a,又
+
=1,
即有a=
,b=3,取得最小值,且为16.
故答案为:16.
| 1 |
| a |
| 1 |
| b |
则有
| 1 |
| a |
| 1 |
| b |
| b-1 |
| b |
则有
| 1 |
| b-1 |
| a |
| b |
| 1 |
| b |
| 1 |
| a |
| a-1 |
| a |
| 1 |
| a-1 |
| b |
| a |
则有
| 4 |
| a-1 |
| 16 |
| b-1 |
| 4b |
| a |
| 16a |
| b |
|
当且仅当
| 4b |
| a |
| 16a |
| b |
| 1 |
| a |
| 1 |
| b |
即有a=
| 3 |
| 2 |
故答案为:16.
点评:本题考查基本不等式的运用:求最值,考查化简变形的能力,属于中档题和易错题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
某社团有男生30名,女生20名,从中抽取一个容量为5的样本,恰好抽到2名男生和3名女生,则
①该抽样一定不是系统抽样;
②该抽样可能是随机抽样;
③该抽样不可能是分层抽样;
④男生被抽到的概率大于女生被抽到的概率;
其中说法正确的为( )
①该抽样一定不是系统抽样;
②该抽样可能是随机抽样;
③该抽样不可能是分层抽样;
④男生被抽到的概率大于女生被抽到的概率;
其中说法正确的为( )
| A、①②③ | B、②③ | C、③④ | D、①④ |
已知抛物线y2=2px(p>0)与双曲线
-
=1(a>0,b>0)有共同的焦点F,P为抛物线与双曲线的一个交点,且∠PFO=
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
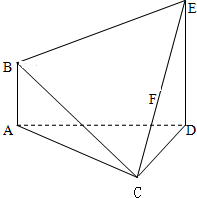 如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AC=CD=7,AD=7,求多面体ABEDC的体积.
如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AC=CD=7,AD=7,求多面体ABEDC的体积.