题目内容
6.在△ABC中,有①$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$;
②$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{0}$;
③若($\overrightarrow{AB}+\overrightarrow{AC})•(\overrightarrow{AB}-\overrightarrow{AC})=0$•($\overrightarrow{AB}-\overrightarrow{AC})$=0,则△ABC是等腰三角形;
④若$\overrightarrow{AB}•\overrightarrow{AC}>0$,则△ABC为锐角三角形.
上述命题正确的是( )
| A. | ①② | B. | ①④ | C. | ②③ | D. | ②③④ |
分析 根据向量的运算性质分别判断即可.
解答 解:对于①$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$,错误,应是$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{CB}$;
②$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{0}$,正确;
③若($\overrightarrow{AB}+\overrightarrow{AC})•(\overrightarrow{AB}-\overrightarrow{AC})=0$•($\overrightarrow{AB}-\overrightarrow{AC})$=0,则${\overrightarrow{AB}}^{2}$-${\overrightarrow{AC}}^{2}$=0,
∴|$\overrightarrow{AB}$|2=|$\overrightarrow{AC}$|2,故AB=AC,
△ABC为等腰三角形,故③正确;
④若$\overrightarrow{AB}•\overrightarrow{AC}>0$,则△ABC不一定是锐角三角形,
故④错误;
故选:C.
点评 本小题主要考查向量的数量积、向量的模、向量在几何中的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
7.下列命题正确的是( )
| A. | 若a2>b2,则a>b | B. | 若ac>bc,则a>b | C. | 若$\frac{1}{a}>\frac{1}{b},则a<b$ | D. | 若$\sqrt{a}<\sqrt{b},则a<b$ |
18.已知f(x)(x∈R)有导函数,且?x∈R,f′(x)>f(x),n∈N*,则有( )
| A. | enf(-n)<f(0),f(n)>enf(0) | B. | enf(-n)<f(0),f(n)<enf(0) | ||
| C. | enf(-n)>f(0),f(n)>enf(0) | D. | enf(-n)>f(0),f(n)<enf(0) |
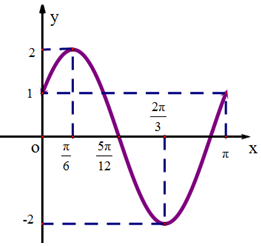 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示. 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.